Question

【题目】已知函数f（x）满足f（x）=f（ ），当x∈[1，4]时，f（x）=lnx，若在区间x∈[ ，4]内，函数g（x）=f（x）﹣ax与x轴有三个不同的交点，则实数a的取值范围是 ．

Answer 1

【答案】
【解析】解：当x∈[ ，1]时，f（x）=f（ ）=ln ，

作出f（x）在[ ，4]上的函数图象如图所示：

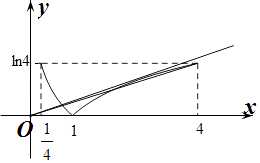
∵g（x）=f（x）﹣ax在[ ，4]上又3个交点，

∴f（x）与y=ax有3个交点，

若直线y=ax经过点（4，ln4），则a= = ，

若直线y=ax与y=lnx相切，设切点为（x，y），则 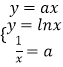，解得 ，

∴ ≤a＜ ．

所以答案是： ．

【考点精析】解答此题的关键在于理解函数的图象的相关知识，掌握函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值．