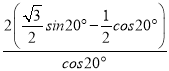题目内容
【题目】在直三棱柱ABC﹣A1B1C1中,∠ABC=90°,E、F分别为A1C1、B1C1的中点,D为棱CC1上任一点.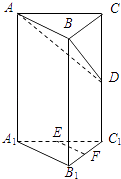
(Ⅰ)求证:直线EF∥平面ABD;
(Ⅱ)求证:平面ABD⊥平面BCC1B1 .
【答案】证明:(Ⅰ)因为E、F分别为A1C1,B1C1的中点,所以EF∥A1B1∥AB
而EF面ABD,AB面ABD,所以直线EF∥平面ABD
(Ⅱ)因为三棱柱ABC﹣A1B1C1为直三棱柱,所以AB⊥BB1,又AB⊥BC,
而BB1面BCC1B1,BC面BCC1B1,且BB1∩BC=B,所以AB⊥面BCC1B1
又AB面ABD,所以平面ABD⊥平面BCC1B1
【解析】(I)先证明EF∥AB,再利用线面平行的判定定理可证明直线EF∥平面ABD;(II)先证明AB⊥面BCC1B1,再证明平面ABD⊥平面BCC1B1.
【考点精析】关于本题考查的直线与平面平行的判定和平面与平面垂直的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直才能得出正确答案.

练习册系列答案
相关题目