题目内容
已知集合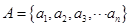 ,
,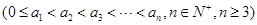
具有性质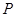 :对任意的
:对任意的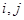
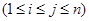 ,
,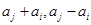 至少有一个属于
至少有一个属于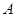 .
.
(1)分别判断集合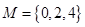 与
与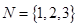 是否具有性质
是否具有性质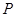 ;
;
(2)求证:①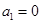 ;
;
②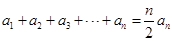 ;
;
(3)当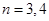 或
或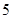 时集合
时集合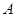 中的数列
中的数列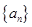 是否一定成等差数列?说明理由.
是否一定成等差数列?说明理由.
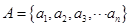 ,
,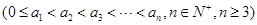
具有性质
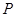 :对任意的
:对任意的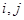
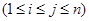 ,
,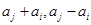 至少有一个属于
至少有一个属于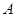 .
.(1)分别判断集合
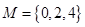 与
与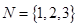 是否具有性质
是否具有性质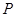 ;
;(2)求证:①
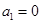 ;
;②
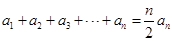 ;
;(3)当
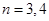 或
或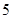 时集合
时集合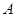 中的数列
中的数列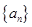 是否一定成等差数列?说明理由.
是否一定成等差数列?说明理由.(1)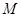 有 ,
有 ,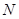 没有;(2)证明见解析;(3)
没有;(2)证明见解析;(3)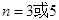 时,是等差数列,
时,是等差数列,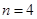 时,不一定.
时,不一定.
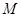 有 ,
有 ,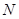 没有;(2)证明见解析;(3)
没有;(2)证明见解析;(3)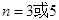 时,是等差数列,
时,是等差数列,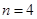 时,不一定.
时,不一定.试题分析:(1)对于具体的集合
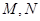 ,我们根据定义直接验证即可,如集合
,我们根据定义直接验证即可,如集合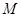 ,
,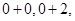
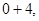
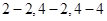 均属于集合
均属于集合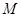 ,故
,故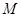 个有性质
个有性质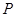 ,而集合
,而集合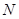 ,
,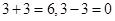 均不属于
均不属于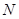 ,则
,则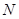 不具有性质
不具有性质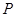 ;(2)
;(2)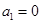 易证,等式
易证,等式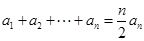 变形得
变形得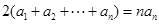 ,联想到等差数列的前
,联想到等差数列的前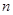 项和求法,是不是有
项和求法,是不是有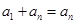 (这是成立的),
(这是成立的),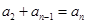 (?),
(?),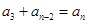 (?),…,由于
(?),…,由于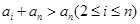 ,故
,故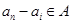 ,从而可看出只能是
,从而可看出只能是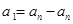 ,
, ,
,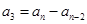 ,…,
,…,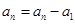 ,即
,即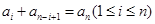 成立,②式得证;(3)如果答案是肯定的,必须证明,如果答案是不确定的,则要举例说明,
成立,②式得证;(3)如果答案是肯定的,必须证明,如果答案是不确定的,则要举例说明,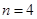 时,集合
时,集合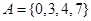 具有性质
具有性质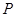 ,但不是等差数列,
,但不是等差数列,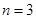 和
和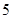 时,具有性质
时,具有性质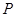 的集合
的集合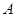 中的数列是等差数列,
中的数列是等差数列,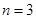 时易证,首先
时易证,首先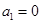 ,然后
,然后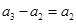 ,即
,即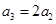 ,故
,故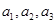 成等差,
成等差,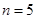 时,难一点,由(2)知
时,难一点,由(2)知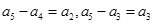 ,两式相减可得
,两式相减可得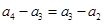 ,而由于
,而由于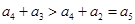 ,即
,即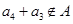 ,则有
,则有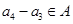 ,注意到
,注意到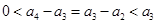 ,于是
,于是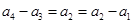 ,又有
,又有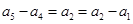 ,故数列
,故数列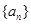 是等差数列,
是等差数列,试题解析:(1)∵
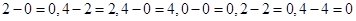 ≒∴集合
≒∴集合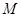 具有性质
具有性质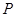 ,
,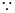
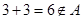 ,
,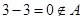 ,
,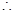 集合
集合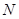 不具有性质
不具有性质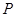 . 3分
. 3分(2)由已知
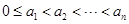 ,
,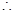
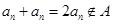 ,
,则
 ,仍由
,仍由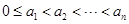 知
知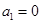 ; 5分
; 5分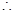

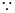
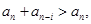
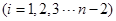 ,
,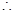
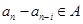 ,
,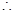
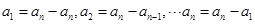 6分
6分将上述各式两边相加得
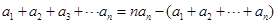
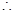
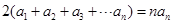 ,即
,即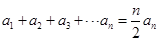 ; 8分
; 8分(3)当
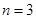 时,集合
时,集合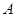 中的数列
中的数列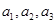 一定是等差数列.
一定是等差数列.由(2)知
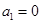 ,且
,且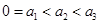 ,
,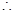
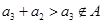
故
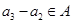 ,而这里
,而这里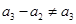 ,反之若不然
,反之若不然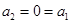
这与集合
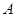 中元素互异矛盾,
中元素互异矛盾,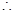 只能
只能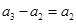 ,即
,即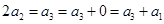
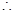
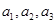 成等差数列. 9分
成等差数列. 9分当
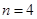 时,集合
时,集合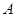 中的元素
中的元素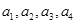 不一定是等差数列.
不一定是等差数列.如
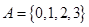 ,
,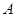 中元素成等差数列,
中元素成等差数列,又如
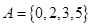 ,
,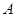 中元素不成等差数列; 11分
中元素不成等差数列; 11分当5时,集合
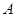 中的元素
中的元素 一定成等差数列
一定成等差数列 证明:
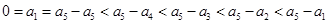
令
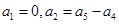 ①
①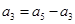 ②
②②
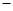 ①有
①有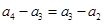 ,且由①
,且由①
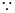
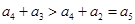 ,
,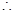
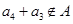
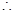
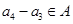
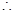
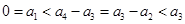 ,
,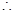
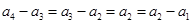
又
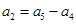 ,
,
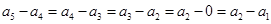
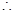
 成等差数列. 13分
成等差数列. 13分
练习册系列答案
相关题目
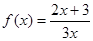 , 数列
, 数列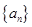 满足
满足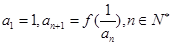 .
.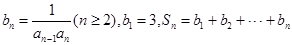 ,若
,若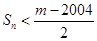 对一切
对一切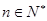 成立,求最小正整数m.
成立,求最小正整数m.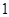 的等比数列
的等比数列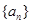 的首项
的首项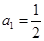 ,前
,前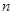 项和为
项和为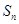 ,且
,且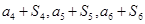 成等差数列.
成等差数列.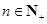 ,在
,在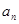 与
与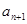 之间插入
之间插入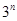 个数,使这
个数,使这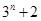 个数成等差数列,记插入的这
个数成等差数列,记插入的这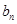 ,求数列
,求数列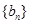 的前
的前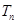 .
.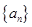 是首项为
是首项为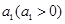 ,公差为
,公差为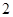 的等差数列,其前
的等差数列,其前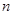 项和为
项和为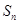 ,且
,且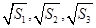 成等差数列.
成等差数列.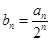 的前
的前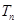 ,求
,求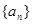 满足
满足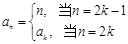 ,其中
,其中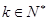 ,设
,设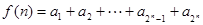 ,则
,则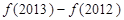 等于( )
等于( )



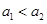 ,
,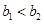 ,且
,且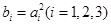 ,则
,则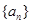 ,
,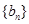 的前
的前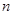 项和分别为
项和分别为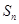 ,
,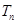 ,若
,若 ,则
,则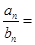 ( )
( )



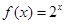 ,等差数列
,等差数列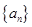 的公差为
的公差为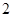 ,a1=1,则
,a1=1,则