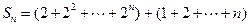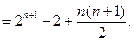题目内容
(本题14分)
已知数列 的首项
的首项 ,通项
,通项 ,且成等差数列。求:
,且成等差数列。求:
(Ⅰ)p,q的值;
(Ⅱ) 数列 前n项和
前n项和 的公式。
的公式。
已知数列
 的首项
的首项 ,通项
,通项 ,且成等差数列。求:
,且成等差数列。求:(Ⅰ)p,q的值;
(Ⅱ) 数列
 前n项和
前n项和 的公式。
的公式。(Ⅰ)p=1,q=1
(Ⅱ)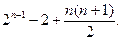
(Ⅱ)
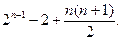
本题主要考查等差数列和等比数列的基本知识,考查运算及推理能力。满分14分。
(Ⅰ)由
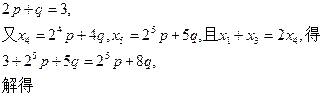 Ⅱ
Ⅱ
p=1,q=1
(Ⅱ)解: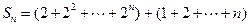
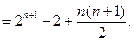
(Ⅰ)由

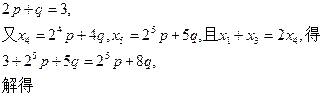 Ⅱ
Ⅱp=1,q=1
(Ⅱ)解:
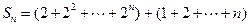
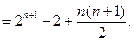

练习册系列答案
相关题目
题目内容
 的首项
的首项 ,通项
,通项 ,且成等差数列。求:
,且成等差数列。求: 前n项和
前n项和 的公式。
的公式。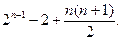

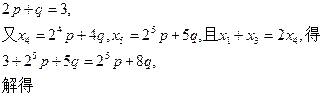 Ⅱ
Ⅱ