题目内容
7．已知圆（x-$\frac{1}{2}$）2+（y-3）2=$\frac{25}{4}$与直线x+2y-3=0的两个交点为P，Q，求以PQ为直径的圆的方程．分析 运用了“圆系方程”，求出圆心坐标，由圆心在直线x+2y-3=0上，即可得出结论．
解答 解：圆的方程可化为x2+y2+x-6y+3=0，设所求圆的方程为x2+y2+x-6y+3+λ（x+2y-3）=0，
整理，得：x2+y2+（1+λ）x+（2λ-6）y+3-3λ=0，
此圆的圆心坐标是：（-$\frac{1+λ}{2}$，3-λ），
由圆心在直线x+2y-3=0上，得-$\frac{1+λ}{2}$+2（3-λ）-3=0
解得λ=1．
故所求圆的方程为：x2+y2+2x-4y=0．
点评 运用了“圆系方程”，简化了过程．
练习册系列答案
相关题目
2．函数f（x）=lg（$\frac{1}{\sqrt{{x}^{2}+1}+x}$）的奇偶性是（ ）
| A． | 奇函数 | B． | 偶函数 | C． | 既奇又偶函数 | D． | 非奇非偶函数 |
19．
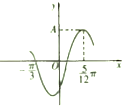函数f（x）=Asin（ωx+φ）的部分图象如图所示，则函数f（x）的周期为（ ）
函数f（x）=Asin（ωx+φ）的部分图象如图所示，则函数f（x）的周期为（ ）| A． | $\frac{π}{2}$ | B． | $\frac{3}{4}π$ | C． | π | D． | 2π |