题目内容
19.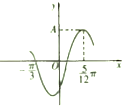 函数f(x)=Asin(ωx+φ)的部分图象如图所示,则函数f(x)的周期为( )
函数f(x)=Asin(ωx+φ)的部分图象如图所示,则函数f(x)的周期为( )| A. | $\frac{π}{2}$ | B. | $\frac{3}{4}π$ | C. | π | D. | 2π |
分析 由函数f(x)=Asin(ωx+φ)的部分图象,可得$\frac{3T}{4}$=$\frac{3}{4}•\frac{2π}{ω}$=$\frac{5π}{12}$-(-$\frac{π}{3}$),由此求得周期T的值.
解答 解:由函数f(x)=Asin(ωx+φ)的部分图象,可得$\frac{3T}{4}$=$\frac{3}{4}•\frac{2π}{ω}$=$\frac{5π}{12}$-(-$\frac{π}{3}$)=$\frac{3π}{4}$,
求得周期T=π,
故选:C.
点评 本题主要考查正弦函数的周期性,属于基础题.

练习册系列答案
相关题目
10.已知x,y∈R+,且x+2y=$\sqrt{3}$,则$\frac{xy+1}{{x}^{2}+4{y}^{2}}$的最大值为( )
| A. | $\frac{11}{12}$ | B. | $\frac{11}{6}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
14.集合A中的元素y满足y∈N,且y=-x2+1,若t∈A,则t的值为( )
| A. | 0 | B. | 1 | C. | 0或1 | D. | 小于等于1 |
4.已知实数x,y满足$\left\{\begin{array}{l}{x-2y+1≥0}\\{x<2}\\{x+y-1≥0}\end{array}\right.$,则z=2x-2y-1的取值范围是( )
| A. | [$\frac{5}{3}$,5] | B. | [-$\frac{5}{3}$,5) | C. | [$\frac{5}{3}$,5) | D. | [0,5] |
8.已知全集U=R,集合A={x|-2≤x≤3},B={x|x<-2或x>4},那么集合(∁UA)∩(∁UB)等于( )
| A. | {x|3<x≤4} | B. | {x|x≤3或x≥4} | C. | {x|3≤x<4} | D. | {x|-1≤x≤3} |
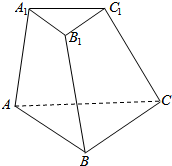 如图所示的是一个三棱台ABC-A1B1C1,如何用两个平面把这个三棱台分成三部分,使每一部分都是一个三棱锥.
如图所示的是一个三棱台ABC-A1B1C1,如何用两个平面把这个三棱台分成三部分,使每一部分都是一个三棱锥.