题目内容
12.设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别是F1和F2,离心率e=$\frac{{\sqrt{2}}}{2}$,点F2到右准线l的距离为$\sqrt{2}$.(Ⅰ)求a、b的值;
(Ⅱ)设M、N是右准线l上两动点,满足$\overrightarrow{{F_1}M}•\overrightarrow{{F_2}N}$=0.当|MN|取最小值时,求证:M,N两点关于x轴对称.
分析 (Ⅰ)运用离心率公式和准线方程,结合a,b,c的关系,可得a,b;
(Ⅱ)求出椭圆的左右焦点坐标,求出右准线方程,设出M,N的坐标,运用向量的数量积的坐标表示,可得y1y2=-6,由基本不等式求出|MN|的最小值,即可得证.
解答 解:(1)因为$e=\frac{c}{a}$,F2到l的距离$d=\frac{a^2}{c}-c$,
所以由题设得$\left\{\begin{array}{l}\frac{c}{a}=\frac{{\sqrt{2}}}{2}\\ \frac{a^2}{c}-c=\sqrt{2}\end{array}\right.$,
解得,$c=\sqrt{2},a=2$.
由${b^2}={a^2}-{c^2}=2,得b=\sqrt{2}$.
(Ⅱ)证明:由$c=\sqrt{2}$,a=2得${F_1}(-\sqrt{2},0),{F_2}(\sqrt{2},0)$.
则l的方程为$x=2\sqrt{2}$.
故可设$M(2\sqrt{2},{y_1}),N(2\sqrt{2},{y_2})$.
$\overrightarrow{{F}_{1}M}$=(2$\sqrt{2}$+$\sqrt{2}$,y1),$\overrightarrow{{F}_{2}N}$=(2$\sqrt{2}$-$\sqrt{2}$,y2),
由$\overrightarrow{{F_1}M}•\overrightarrow{{F_2}N}$=0知,3$\sqrt{2}$×$\sqrt{2}$+y1y2=0,
得y1y2=-6,所以y1y2≠0,
${y_2}=-\frac{6}{y_1}$,|$\overrightarrow{MN}$|=|y1-y2|=|y1+$\frac{6}{{y}_{1}}$|=|y1|+$\frac{6}{|{y}_{1}|}$$≥2\sqrt{6}$,
当且仅当${y_1}=±\sqrt{6}$时,上式取等号,此时y1=-y2.
即M,N两点关于x轴对称.
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率和准线方程的运用,同时考查向量的数量积的坐标表示和基本不等式的运用,属于中档题.

| A. | {1} | B. | {5} | C. | {2,4} | D. | {1,2,4,5} |
| A. | (0,1) | B. | (1,2) | C. | (2,e) | D. | (3,4) |
| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{12}$ |
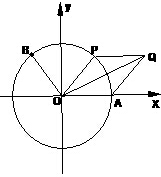 如图,点A是单位圆与x轴正半轴的交点,B(-$\frac{3}{5}$,$\frac{4}{5}$).
如图,点A是单位圆与x轴正半轴的交点,B(-$\frac{3}{5}$,$\frac{4}{5}$).