题目内容
13.已知-π2<α<0<β<π2,cos(a-β)=35,sinβ=513,tanα=-3356.分析 根据已知条件,利用同角三角函数间的基本关系求出cosβ与sin(α-β)的值,利用两角和与差的正弦、余弦函数公式求出sinα与cosα的值,即可求出tanα的值.
解答 解:∵-π2<α<0<β<π2,cos(a-β)=35,sinβ=513,
∴sin(α-β)=-√1−(35)2=-45,cosβ=√1−(513)2=1213,
∴cosα=cos[(α-β)+β]=cos(α-β)cosβ-sin(α-β)sinβ=35×1213+45×513=5665,
sinα=sin[(α-β)+β]=sin(α-β)cosβ+cos(α-β)sinβ=-45×1213+35×513=-3365,
则tanα=-3356,
故答案为:-3356
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
3.函数f(x)=log2(x+2)-3x(x>0)的零点所在的大致区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,e) | D. | (3,4) |
1.一只小狗在如图所示的方砖上走来走去,求最终停在阴影方砖上的概率为( )
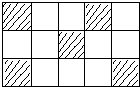

| A. | 310 | B. | 15 | C. | 13 | D. | 512 |
3.执行如图的程序框图,若输出的k=2,则输入x的取值范围是( )
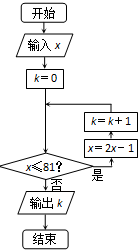

| A. | (21,41) | B. | [21,41] | C. | (21,41] | D. | [21,41) |
 甲、乙两人在9天每天加工零件的个数用茎叶图表示如图,则这9天甲、乙加工零件个数的中位数之和为91.(考点:茎叶图与中位数综合)
甲、乙两人在9天每天加工零件的个数用茎叶图表示如图,则这9天甲、乙加工零件个数的中位数之和为91.(考点:茎叶图与中位数综合)