题目内容
已知圆心为C（6，5），且过点B（3，6）的圆的方程为
A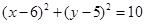． | B． |
C． | D． |
A.
解析试题分析：因为圆心为C（6，5）,所以所求圆的方程为
,因为此圆过点B（3，6），
所以
,所以
，因而所求圆的方程为.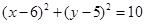
考点：圆的标准方程.
点评：在知道圆心的情况下可设圆的标准方程为,然后根据圆过点B（3，6），
代入方程可求出r的值，得到圆的方程.
练习册系列答案
能力评价系列答案
相关题目
已知圆
，直线
，则圆C内任意一点到直线的距离小于
的概率为（ ）
A． | B． | C． | D． |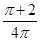
圆
上的点到直线
的距离最大值是( )
| A．2 | B． | C． | D． |
直线
被圆
所截得的弦长为( )
A． | B． | C． | D． |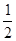
设
,
,若直线
与圆
相切,则
的取值范
围是（ ）
A． | B． |
C． | D． |
设A，B为直线
与圆
的两个交点，则|AB|=( )
| A．1 | B． | C． | D．2 |
若圆
始终平分圆
的周长, 则a、b应满足的关系式是
A． 0 | B． 0 |
C． 0 | D． 0 |
直线x+y+1=0与圆
的位置关系是
| A．相交 | B．相离 | C．相切 | D．不能确定 |
过两圆：x2 + y 2 + 6 x + 4y = 0及x2+y 2 + 4x + 2y – 4 =0的交点的直线的方程
| A．x+y+2=0 | B．x+y-2="0" |
| C．5x+3y-2=0 | D．不存在 |