题目内容
已知 ,点
,点
 是圆
是圆 内一点,直线
内一点,直线 是以点
是以点 为中点的弦所在的直线,直线
为中点的弦所在的直线,直线 的方程是
的方程是 ,则下列结论正确的是( )
,则下列结论正确的是( )
A. ,且 ,且 与圆相交 与圆相交 | B. ,且 ,且 与圆相切 与圆相切 |
C. ,且 ,且 与圆相离 与圆相离 | D. ,且 ,且 与圆相离 与圆相离 |
C
解析试题分析:以点M为中点的弦所在的直线的斜率是-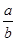 ,直线m∥l,点M(a,b)是圆x2+y2=r2内一点,所以a2+b2<r2,圆心到ax+by=r2,距离是
,直线m∥l,点M(a,b)是圆x2+y2=r2内一点,所以a2+b2<r2,圆心到ax+by=r2,距离是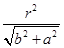 =r,故相离.故选C
=r,故相离.故选C
考点:本题主要是考查直线与圆的位置关系,两条直线的位置关系,是基础题
点评:解决该试题的关键是求圆心到直线的距离,然后与a2+b2<r2比较,可以判断直线与圆的位置关系,易得两直线的关系

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
直线 被圆
被圆 所截得的弦长为( )
所截得的弦长为( )
A. | B. | C. | D.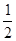 |
设A,B为直线 与圆
与圆 的两个交点,则|AB|=( )
的两个交点,则|AB|=( )
| A.1 | B. | C. | D.2 |
若圆 始终平分圆
始终平分圆 的周长, 则a、b应满足的关系式是
的周长, 则a、b应满足的关系式是
A. 0 0 | B. 0 0 |
C. 0 0 | D. 0 0 |
直线 按向量
按向量 平移后与圆
平移后与圆 相切,则
相切,则 的值等于( )
的值等于( )
A.8或 | B.6或 | C.4或 | D.2或 |
直线x+y+1=0与圆 的位置关系是
的位置关系是
| A.相交 | B.相离 | C.相切 | D.不能确定 |
 和圆
和圆 ,圆心为M,点
,圆心为M,点 在直线
在直线 上,若圆
上,若圆 与直线
与直线 至少有一个公共点
至少有一个公共点 ,且
,且 ,则点
,则点

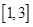

 与圆
与圆 相交于
相交于 两点(其中
两点(其中 是实数),且
是实数),且 是直角三角形(
是直角三角形( 是坐标原点),则点
是坐标原点),则点
 与点
与点
 之间距离的最大值为 ( )
之间距离的最大值为 ( )



 作切线,切点为T,则切线长|PT|的最小值是( )
作切线,切点为T,则切线长|PT|的最小值是( )



