题目内容
过点(1,2)总可作两条直线与圆 相切,则实数
相切,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
C. 或 或 | D.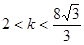 或 或 |
D
解析

练习册系列答案
相关题目
圆 上的点到直线
上的点到直线 的距离最大值是( )
的距离最大值是( )
| A.2 | B. | C. | D. |
若圆 始终平分圆
始终平分圆 的周长, 则a、b应满足的关系式是
的周长, 则a、b应满足的关系式是
A. 0 0 | B. 0 0 |
C. 0 0 | D. 0 0 |
直线x+y+1=0与圆 的位置关系是
的位置关系是
| A.相交 | B.相离 | C.相切 | D.不能确定 |
直线 绕原点按顺时针方向旋转
绕原点按顺时针方向旋转 所得直线与圆
所得直线与圆 的位置关系是( ).
的位置关系是( ).
| A.直线与圆相切 | B.直线与圆相交但不过圆心 |
| C.直线与圆相离 | D.直线过圆心 |
圆 上的点到直线
上的点到直线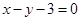 的距离的最大值是( )
的距离的最大值是( )
A. | B. | C. | D.0 |
过两圆:x2 + y 2 + 6 x + 4y = 0及x2+y 2 + 4x + 2y – 4 =0的交点的直线的方程
| A.x+y+2=0 | B.x+y-2="0" |
| C.5x+3y-2=0 | D.不存在 |
双曲线 的渐近线与圆
的渐近线与圆 相切,则
相切,则 等于( )
等于( )
A. | B.2 | C.3 | D.6 |
 与圆
与圆 相交于
相交于 两点(其中
两点(其中 是实数),且
是实数),且 是直角三角形(
是直角三角形( 是坐标原点),则点
是坐标原点),则点
 与点
与点
 之间距离的最大值为 ( )
之间距离的最大值为 ( )


