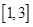题目内容
已知圆C: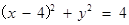 ,从动圆M:
,从动圆M: 上的动点P向圆C引切线,切点分别是E,F,则
上的动点P向圆C引切线,切点分别是E,F,则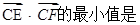 ( )
( )
A. | B. | C. | D. |
A
解析试题分析:根据题意圆C: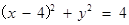 ,其圆心为(4,0),半径为2,从动圆M:
,其圆心为(4,0),半径为2,从动圆M: ,那么动圆的圆心(4+7
,那么动圆的圆心(4+7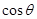 ,7
,7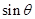 ),那么可知两个圆心的距离为定值,且为
),那么可知两个圆心的距离为定值,且为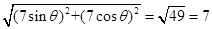 ,连接两圆心与动圆的交点P,此时满足
,连接两圆心与动圆的交点P,此时满足 取得最小值,且为
取得最小值,且为 ,故选A.
,故选A.
考点:本试题考查了直线与圆的位置关系的知识。
点评:对于利用直线与圆相切的问题,一般要用到切线长定理,以及直线与圆的相切时特殊的直角三角形关系,借助于圆心坐标和动点坐标发现规律,两点的距离为定值,来分析最小值。

练习册系列答案
相关题目
直线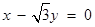 截圆
截圆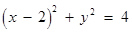 所得劣弧所对的圆心角是
所得劣弧所对的圆心角是
A.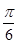 | B.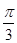 | C.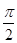 | D.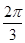 |
已知圆 ,直线
,直线 ,则圆C内任意一点到直线的距离小于
,则圆C内任意一点到直线的距离小于 的概率为( )
的概率为( )
A. | B. | C. | D.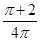 |
直线 与圆
与圆 相交于M、N两点,若
相交于M、N两点,若 ,则k的取值范围为( )
,则k的取值范围为( )
A. | B. | C. | D.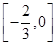 |
已知直线 与圆
与圆 交于
交于 两点,且
两点,且 (其中
(其中 为坐标原点),则实数
为坐标原点),则实数 的值为
的值为
A. | B. | C. 或 或 | D. 或 或 |
圆 上的点到直线
上的点到直线 的距离最大值是( )
的距离最大值是( )
| A.2 | B. | C. | D. |
若圆 始终平分圆
始终平分圆 的周长, 则a、b应满足的关系式是
的周长, 则a、b应满足的关系式是
A. 0 0 | B. 0 0 |
C. 0 0 | D. 0 0 |
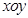 中,圆
中,圆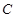 的方程为
的方程为 ,若直线
,若直线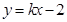 上至少存在一点,使得以该点为圆心,
上至少存在一点,使得以该点为圆心,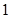 为半径的圆与圆
为半径的圆与圆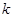 的最大值为
的最大值为 
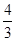


 和圆
和圆 ,圆心为M,点
,圆心为M,点 在直线
在直线 上,若圆
上,若圆 与直线
与直线 至少有一个公共点
至少有一个公共点 ,且
,且 ,则点
,则点