题目内容
若点 为圆
为圆 的弦
的弦 的中点,则直线
的中点,则直线 的方程为( )
的方程为( )
A. | B. |
C. | D. |
D
解析试题分析:因为点 为圆
为圆 的弦
的弦 的中点,
的中点,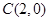 为圆心,所以
为圆心,所以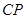 与直线
与直线 垂直,而
垂直,而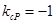 ,所以直线
,所以直线 的斜率为
的斜率为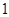 ,所以直线
,所以直线 的方程为
的方程为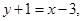 即
即 .
.
考点:本小题主要考查直线与圆相交的性质、两直线垂直的斜率的关系和直线方程的求法,考查学生数形结合思想的应用和运算求解能力.
点评:直线与圆相交时,半径、半弦长和圆心到直线的距离构成一个直角三角形,这是一条很重要也很好用的性质,另外要注意数形结合进行解题可以简化运算.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知直线 与圆
与圆 交于
交于 两点,且
两点,且 (其中
(其中 为坐标原点),则实数
为坐标原点),则实数 的值为
的值为
A. | B. | C. 或 或 | D. 或 或 |
设 ,
, ,若直线
,若直线 与圆
与圆 相切,则
相切,则 的取值范
的取值范
围是( )
A. | B. |
C. | D. |
若圆 始终平分圆
始终平分圆 的周长, 则a、b应满足的关系式是
的周长, 则a、b应满足的关系式是
A. 0 0 | B. 0 0 |
C. 0 0 | D. 0 0 |
若点P(1,1)为圆 的弦MN的中点,则弦MN所在直线的方程为( )
的弦MN的中点,则弦MN所在直线的方程为( )
A. | B. |
C. | D. |
直线x+y+1=0与圆 的位置关系是
的位置关系是
| A.相交 | B.相离 | C.相切 | D.不能确定 |
直线 绕原点按顺时针方向旋转
绕原点按顺时针方向旋转 所得直线与圆
所得直线与圆 的位置关系是( ).
的位置关系是( ).
| A.直线与圆相切 | B.直线与圆相交但不过圆心 |
| C.直线与圆相离 | D.直线过圆心 |
圆 上的点到直线
上的点到直线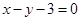 的距离的最大值是( )
的距离的最大值是( )
A. | B. | C. | D.0 |
若直线 (
( )被圆
)被圆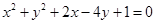 截得的弦长为
截得的弦长为
4,则 的最小值为( )
的最小值为( )
A. | B. | C.2 | D.4 |