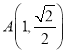题目内容
【题目】已知直线y=b与函数f(x)=2x+3和g(x)=ax+lnx分别交于A,B两点,若AB的最小值为2,则a+b=_______.
【答案】2.
【解析】
设A(x1,b),B(x2,b),则2x1+3=ax2+lnx2=b,表示出x1,求出|AB|,利用导数,结合最小值也为极小值,可得极值点,求出最小值,解方程可得a=1,再求得b和a+b.
设A(x1,b),B(x2,b),可设x1<x2,
则2x1+3=ax2+lnx2=b,
∴x1![]() (ax2+lnx2﹣3),
(ax2+lnx2﹣3),
∴|AB|=x2﹣x1=(1![]() a)x2
a)x2![]() lnx2
lnx2![]() ,
,
令y=(1![]() a)x
a)x![]() lnx
lnx![]() ,
,
则y′=1![]()
![]() (x>0),
(x>0),
由|AB|的最小值为2,
可得2﹣a>0,
函数在(0,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增,
,+∞)上单调递增,
∴x![]() 时,函数y取得极小值,且为最小值2,
时,函数y取得极小值,且为最小值2,
即有(1![]() a)
a)![]() ln
ln![]() 2,即得
2,即得![]() ln
ln![]() 0
0
解得a=1,
由x2=1,
则b=ax2+lnx2=1+ln1=1,
可得a+b=2.
故答案为:2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
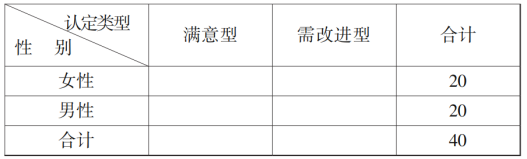
【题目】某调查机构为了解人们某个产品的使用情况是否与性别有关,在网上进行了问卷调查,在调查结果中随机抽取了50份进行统计,得到如下![]() 列联表:
列联表:
男性 | 女性 | 合计 | |
使用 | 15 | 5 | 20 |
不使用 | 10 | 20 | 30 |
合计 | 25 | 25 | 50 |
(1)请根据调查结果分①析:你有多大把握认为使用该产品与性别有关;
(2)在不使用该产品的人中,按性别用分层抽样抽取6人,再从这6人中随机抽取2人参加某项活动,求这2人中恰有一位女性的概率.
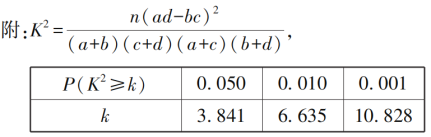
附: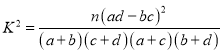
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |