Question

【题目】已知三棱锥内接于球O，平面ABC，为等边三角形，且边长，球的表面积为，则直线PC与平面PAB所成的角的正弦值为

A.B.

C.D.

Answer 1

【答案】D

【解析】

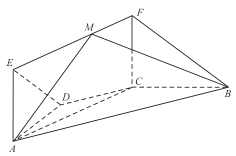
设D为AB中点，先证明CD⊥平面PAB得出∠CPD为所求角，利用勾股定理计算PA，PD，CD，得出结论．

解：设D，E分别是AB，BC的中点，AE∩CD＝F，

∵PA⊥平面ABC，∴PA⊥CD，

∵△ABC是等边三角形，∴CD⊥AB，

又PA∩AB＝A，

∴CD⊥平面PAB，即∠CPD为PC与平面PAB所成的角．

∵△ABC是边长为的等边三角形，

∴CD＝AE＝，AFAE＝1，且F为△平面ABC所在截面圆的圆心，

∵球O的表面积为16π，∴球O的半径OA，

∴OF，

∵PA⊥平面ABC，∴PA＝2OF＝2，

∴PD，PC

∴sin∠CPD．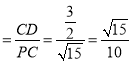

故选：D．