题目内容
【题目】水污染现状与工业废水排放密切相关,某工厂深人贯彻科学发展观,努力提高污水收集处理水平,其污水处理程序如下:原始污水必先经过A系统处理,处理后的污水(A级水)达到环保标准(简称达标)的概率为p(0<p<1).经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放.
某厂现有4个标准水量的A级水池,分别取样、检测,多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验,混合样本中只要有样本不达标,则混合样本的化验结果必不达标,若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放
现有以下四种方案:
方案一:逐个化验;
方案二:平均分成两组化验;方案三;三个样本混在一起化验,剩下的一个单独化验;
方案四:四个样本混在一起化验.
化验次数的期望值越小,则方案越"优".
(1)若![]() ,求2个A级水样本混合化验结果不达标的概率;
,求2个A级水样本混合化验结果不达标的概率;
(2)①若![]() ,现有4个A级水样本需要化验,请问:方案一、二、四中哪个最“优"?②若“方案三”比“方案四"更“优”,求p的取值范围.
,现有4个A级水样本需要化验,请问:方案一、二、四中哪个最“优"?②若“方案三”比“方案四"更“优”,求p的取值范围.
【答案】(1)![]() ;(2)①方案四最优;②
;(2)①方案四最优;②![]()
【解析】
(1)计算2个A级混合样本达标的概率,再根据对立事件原理求得它们不达标的概率;
(2)①计算方案一:逐个检测,检测次数为ξ=4;方案二:检测次数为ξ2,则ξ2可能取值为2,4,6,求概率分布列,计算数学期望;方案四:混在一起检测,检测次数为ξ4,则ξ4可取值为1,5,求概率分布列,计算数学期望;比较得出选择方案几最“优”;
②方案三:化验次数为η3,则η3可取值为2,5,求概率分布列,计算数学期望;
方案四:化验次数为η4,则η4可取值为1,5,求概率分布,计算数学期望;
由题意列不等式E(η3)<E(η4),求出p的取值范围.
(1)该混合样本达标的概率是![]() ,所以根据对立事件原理,不达标的概率为
,所以根据对立事件原理,不达标的概率为![]() .
.
(2)①方案一:逐个检测,检测次数为4.
方案二:由(1)知,每组两个样本检测时,若达标则检测次数为1,概率为![]() ;若不达标则检测次数为3,概率为
;若不达标则检测次数为3,概率为![]() .故方案二的检测次数记为ξ2,ξ2的可能取值为2,4,6.
.故方案二的检测次数记为ξ2,ξ2的可能取值为2,4,6.
其分布列如下,
|
|
|
|
|
|
|
|
可求得方案二的期望为![]()
方案四:混在一起检测,记检测次数为ξ4,ξ4可取1,5.
其分布列如下,
|
|
|
|
|
|
可求得方案四的期望为![]() .
.
比较可得![]() ,故选择方案四最“优”.
,故选择方案四最“优”.
②方案三:设化验次数为![]() ,
,![]() 可取2,5.
可取2,5.
|
|
|
|
|
|
![]() ;
;
方案四:设化验次数为![]() ,
,![]() 可取
可取![]()
|
|
|
|
|
|
![]() ;
;
由题意得![]() .
.
故当![]() 时,方案三比方案四更“优”.
时,方案三比方案四更“优”.

【题目】互联网使我们的生活日益便捷,网络外卖也开始成为不少人日常生活中不可或缺的一部分,某市一调查机构针对该市市场占有率较高的甲、乙两家网络外卖企业(以下外卖甲、外卖乙)的经营情况进行了调查,调查结果如下表:
1日 | 2日 | 3日 | 4日 | 5日 | |
外卖甲日接单x(百单) | 5 | 2 | 9 | 8 | 11 |
外卖乙日接单y(百单) | 2 | 3 | 10 | 5 | 15 |
(1)试根据表格中这五天的日接单量情况,从统计的角度说明这两家外卖企业的经营状况;
(2)据统计表明,y与x之间具有线性关系.
①请用相关系数r对y与x之间的相关性强弱进行判断;(若![]() ,则可认为y与x有较强的线性相关关系(r值精确到0.001))
,则可认为y与x有较强的线性相关关系(r值精确到0.001))
②经计算求得y与x之间的回归方程为![]() ,假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于25百单时,外卖甲所获取的日纯利润的大致范围.(x值精确到0.01)
,假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于25百单时,外卖甲所获取的日纯利润的大致范围.(x值精确到0.01)
相关公式: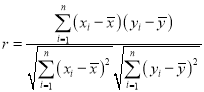 ,
,
参考数据: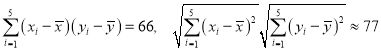 .
.