题目内容
【题目】在正方体ABCD﹣A1B1C1D1中，点E、F、G分别为棱A1D1、A1A、A1B1的中点，给出下列四个命题：①EF⊥B1C；②BC1∥平面EFG；③A1C⊥平面EFG；④异面直线FG、B1C所成角的大小为
．其中正确命题的序号为（ ）
A.①②B.②③C.①②③D.①②④
【答案】C
【解析】
画出正方体的直观图，结合线面平行与垂直的判定定理和性质定理逐项判断即可得到正确选项.
如图，
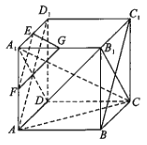
正方体ABCD﹣A1B1C1D1中，A1D//B1C，又A1D⊥EF，故B1C⊥EF，即①正确；
又BC1∥AD1，AD1//EF，故BC1//EF，又EF平面EFG，故BC1∥平面EFG，即②正确；
因为EF⊥A1D，EF⊥A1B1，所以EF⊥平面A1B1CD，又A1C 平面A1B1CD，所以EF⊥A1C，同理可证EG⊥A1C，又EF∩EG=E，EF平面EFG，EG平面EFG，故A1C⊥平面EFG，即③正确；
连接AB1，则AB1//FG，故∠AB1C为异面直线FG与B1C所成角，且∠AB1C=
，即④错误.
故所有正确命题的序号为①②③.
故选：C.
练习册系列答案
相关题目
