题目内容
【题目】已知动点M到定点![]() 的距离和它到直线
的距离和它到直线![]() 的距离的比是常数
的距离的比是常数![]() .
.
(1)求动点M的轨迹方程;
(2)令(1)中方程表示曲线C,点S(2,0),过点B(1,0)的直线l与曲线C相交于P,Q两点,求△PQS的面积的取值范围.
【答案】(1)![]() ,(2) 0<S
,(2) 0<S![]() .
.
【解析】
(1)设M(x,y),直接根据距离比计算得到答案.
(2)设直线l:x=ky+1,联立方程,利用韦达定理得到y1+y2![]() ,y1y2
,y1y2![]() ,令t
,令t![]() ,则|AB|=4
,则|AB|=4![]() ,计算得到答案.
,计算得到答案.
(1)设M(x,y),由题意得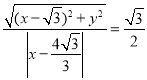 ,得
,得![]() ,
,
(2)设直线l:x=ky+1,由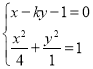 ,消去x得(4+k2)y2+2ky﹣3=0,
,消去x得(4+k2)y2+2ky﹣3=0,
y1+y2![]() ,y1y2
,y1y2![]() ,
,
|PQ |![]() |y1﹣y2|
|y1﹣y2|![]() 4
4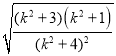 ,
,
令t![]() ∈(0,
∈(0,![]() ],
],
上式化简为:|PQ |=4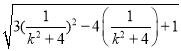 |=4
|=4![]() ,
,
函数在定义域内单调递减,故当t![]() ,有最大值
,有最大值![]() ,
,
所以0<S![]() .
.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
【题目】某蛋糕店计划按天生产一种面包,每天生产量相同,生产成本每个6元,售价每个8元,未售出的面包降价处理,以每个5元的价格当天全部处理完.
(1)若该蛋糕店一天生产30个这种面包,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:个,
(单位:个,![]() )的函数解析式;
)的函数解析式;
(2)蛋糕店记录了30天这种面包的日需求量(单位:个),整理得下表:
日需求量 | 28 | 29 | 30 | 31 | 32 | 33 |
频数 | 3 | 4 | 6 | 6 | 7 | 4 |
假设蛋糕店在这30天内每天生产30个这种面包,求这30天的日利润(单位:元)的平均数及方差.