Question

【题目】综合题。
（1）设不等式（x﹣a）（x+a﹣2）＜0的解集为N， ，若x∈N是x∈M的必要条件，求a的取值范围．
（2）已知命题：“x∈{x|﹣1＜x＜1}，使等式x2﹣x﹣m=0成立”是真命题，求实数m的取值范围．

Answer 1

【答案】
（1）解：因为x∈N是x∈M的必要条件，所以MN，

当a=1时，解集N为空集、不满足题意；

当a＞1时，a＞2﹣a，此时集合N={x|2﹣a＜x＜a}，

则 ，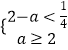

所以

（2）解：由题意得，方程x2﹣x﹣m=0在（﹣1，1）上有解，

∴m的取值集合就是函数y=x2﹣x=（x﹣ ）2﹣ 在（﹣1，1）上的值域，值域为[﹣ ，2），

∴实数m的取值范围[﹣ ，2）

【解析】（1）∈N是x∈M的必要条件，所以MN，当a=1时，解集N为空集，不满足，当a＞1时，求得解集，列不等式组即可求得a的取值范围；（2）方程x2﹣x﹣m=0在（﹣1，1）上有解，m的取值集合就是函数y=x2﹣x=（x﹣ ）2﹣ 在（﹣1，1）上的值域，根据二次函数性质，即可求得实数m的取值范围．
【考点精析】关于本题考查的命题的真假判断与应用，需要了解两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系才能得出正确答案．