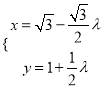题目内容
【题目】已知c>0,设命题p:函数y=cx为减函数.命题q:当x∈[ ![]() ,2]时,函数f(x)=x+
,2]时,函数f(x)=x+ ![]() >
> ![]() 恒成立.如果“p或q”为真命题,“p且q”为假命题,则c的取值范围是 .
恒成立.如果“p或q”为真命题,“p且q”为假命题,则c的取值范围是 .
【答案】![]()
【解析】解:若命题p:函数y=cx为减函数为真,
则c∈(0,1),
x∈[ ![]() ,2]时,函数f(x)=x+
,2]时,函数f(x)=x+ ![]() ∈[2,
∈[2, ![]() ]
]
若命题q:当x∈[ ![]() ,2]时,函数f(x)=x+
,2]时,函数f(x)=x+ ![]() >
> ![]() 恒成立为真,
恒成立为真,
则2> ![]() ,则c∈(
,则c∈( ![]() ,+∞),
,+∞),
∵“p或q”为真命题,“p且q”为假命题,
故p,q一真一假,
若p真q假,则c∈(0, ![]() ],
],
若p假q真,则c∈[1,+∞),
故c的取值范围是: ![]() ,
,
所以答案是: ![]()
【考点精析】掌握命题的真假判断与应用是解答本题的根本,需要知道两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目