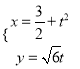题目内容
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,圆
,圆![]() 的极坐标方程为
的极坐标方程为![]() ,已知
,已知![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 位于第一象限.
位于第一象限.
(Ⅰ)求点![]() 和点
和点![]() 的极坐标;
的极坐标;
(Ⅱ)设圆![]() 的圆心为
的圆心为![]() ,点
,点![]() 是直线
是直线![]() 上的动点,且满足
上的动点,且满足![]() ,若直线
,若直线![]() 的参数方程为
的参数方程为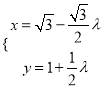 (
(![]() 为参数),则
为参数),则![]() 的值为多少?
的值为多少?
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)联立![]() 与
与![]() 的极坐标方程解得点
的极坐标方程解得点![]() 和点
和点![]() 的极坐标;(2)点
的极坐标;(2)点![]() 的直角坐标为
的直角坐标为![]() ,
, ![]() ,设点
,设点![]() 对应的参数为
对应的参数为![]() ,即
,即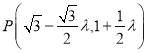 ,由
,由![]() ,求得
,求得![]() 的值.
的值.
试题解析:
解:(Ⅰ)联立![]() 与
与![]() 的极坐标方程
的极坐标方程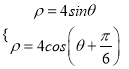 ,得
,得![]() ,
,
当![]() 时,得交点
时,得交点![]() 极坐标为
极坐标为![]() ,
,
当![]() 时,化简得
时,化简得![]() ,从而
,从而![]() ,
, ![]() 或
或![]() ,
, ![]() (舍去),
(舍去),
∴点![]() 的极坐标是
的极坐标是![]() .
.
(Ⅱ)由(Ⅰ)得点![]() 的直角坐标为
的直角坐标为![]() ,
,
将圆![]() 的极坐标方程化为直角坐标方程得
的极坐标方程化为直角坐标方程得![]() ,从而
,从而![]() 的直角坐标为
的直角坐标为![]() ,
,
设点![]() 对应的参数为
对应的参数为![]() ,即
,即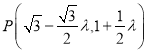 ,
,
则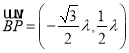 ,
, ![]() ,由
,由![]() ,得
,得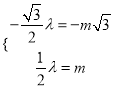 ,
,
∴![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目