题目内容
【题目】下列命题中:①、若m>0,则方程x2﹣x+m=0有实根. ②、若x>1,y>1,则x+y>2的逆命题. ③、对任意的x∈{x|﹣2<x<4},|x﹣2|<3的否定形式. ④、△>0是一元二次方程ax2+bx+c=0有一正根和一负根的充要条件.是真命题的有 .
【答案】③
【解析】解:对于①:方程x2﹣x+m=0有实根,
∴△=1﹣4m≥0,
∴ ![]() ,
,
∴该命题是假命题;
对于②:该命题的逆命题为:
若x+y>2,则x>1,y>1.
举反例:取x=﹣3,y=8,满足x+y>2,
但是推不出x>1,y>1.
∴该命题是假命题;
对于③:对任意的x∈{x|﹣2<x<4},|x﹣2|<3的否定形式为:
存在x∈{x|﹣2<x<4},|x﹣2|≥3,
∵﹣2<x<4,
∴﹣4<x﹣2<2,∴|x﹣2|<4,
∴存在这样的x,满足条件,故③为真命题;
对于④:若方程有一正根和一负根,则满足 ![]() ,
,
∴该命题是假命题;
所以答案是③.
【考点精析】掌握命题的真假判断与应用是解答本题的根本,需要知道两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案【题目】【2017湖南长沙二模】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
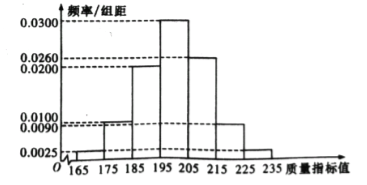
(1)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(2)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
【题目】【2017河北唐山二模】某仪器经过检验合格才能出厂,初检合格率为![]() :若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为
:若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为![]() .每台仪器各项费用如表:
.每台仪器各项费用如表:
项目 | 生产成本 | 检验费/次 | 调试费 | 出厂价 |
金额(元) | 1000 | 100 | 200 | 3000 |
(Ⅰ)求每台仪器能出厂的概率;
(Ⅱ)求生产一台仪器所获得的利润为1600元的概率(注:利润![]() 出厂价
出厂价![]() 生产成本
生产成本![]() 检验费
检验费![]() 调试费);
调试费);
(Ⅲ)假设每台仪器是否合格相互独立,记![]() 为生产两台仪器所获得的利润,求
为生产两台仪器所获得的利润,求![]() 的分布列和数学期望.
的分布列和数学期望.