题目内容
【题目】如图,已知抛物线C:y2=2px和⊙M:(x﹣4)2+y2=1,过抛物线C上一点H(x0 , y0)(y0≥1)作两条直线与⊙M相切于A、两点,分别交抛物线为E、F两点,圆心点M到抛物线准线的距离为 ![]() .
.
(Ⅰ)求抛物线C的方程;
(Ⅱ)当∠AHB的角平分线垂直x轴时,求直线EF的斜率;
(Ⅲ)若直线AB在y轴上的截距为t,求t的最小值.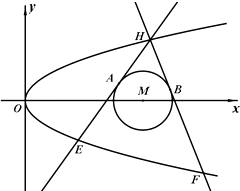
【答案】解:(Ⅰ)∵点M到抛物线准线的距离为 ![]() =
= ![]() ,
,
∴ ![]() ,∴抛物线C的方程为y2=x.
,∴抛物线C的方程为y2=x.
(Ⅱ)法一:∵当∠AHB的角平分线垂直x轴时,点H(4,2),∴kHE=﹣kHF ,
设E(x1 , y1),F(x2 , y2),∴ ![]() ,∴
,∴ ![]() ,
,
∴y1+y2=﹣2yH=﹣4.
∴ ![]() .
.
法二:∵当∠AHB的角平分线垂直x轴时,点H(4,2),∴∠AHB=60°,可得 ![]() ,
, ![]() ,
,
∴直线HA的方程为 ![]() ,
,
联立方程组  ,得
,得 ![]() ,
,
∵ ![]()
∴ ![]() ,
, ![]() .
.
同理可得 ![]() ,
, ![]() ,∴
,∴ ![]() .(
.(
(Ⅲ)法一:设A(x1 , y1),B(x2 , y2),∵ ![]() ,∴
,∴ ![]() ,
,
∴直线HA的方程为(4﹣x1)x﹣y1y+4x1﹣15=0,
同理,直线HB的方程为(4﹣x2)x﹣y2y+4x2﹣15=0,
∴ ![]() ,
, ![]() ,
,
∴直线AB的方程为 ![]() ,
,
令x=0,可得 ![]() ,
,
∵ ![]() ,∴t关于y0的函数在[1,+∞)上单调递增,
,∴t关于y0的函数在[1,+∞)上单调递增,
∴当y0=1时,tmin=﹣11.
法二:设点H(m2 , m)(m≥1),HM2=m4﹣7m2+16,HA2=m4﹣7m2+15.
以H为圆心,HA为半径的圆方程为(x﹣m2)2+(y﹣m)2=m4﹣7m2+15,①
⊙M方程:(x﹣4)2+y2=1.②
①﹣②得:直线AB的方程为(2x﹣m2﹣4)(4﹣m2)﹣(2y﹣m)m=m4﹣7m2+14.(9分)
当x=0时,直线AB在y轴上的截距 ![]() (m≥1),
(m≥1),
∵ ![]() ,∴t关于m的函数在[1,+∞)上单调递增,
,∴t关于m的函数在[1,+∞)上单调递增,
∴当m=1时,tmin=﹣11
【解析】(Ⅰ)利用点M到抛物线准线的距离为 ![]() ,可得
,可得 ![]() ,从而可求抛物线C的方程;(Ⅱ)法一:根据当∠AHB的角平分线垂直x轴时,点H(4,2),可得kHE=﹣kHF , 设E(x1 , y1),F(x2 , y2),可得y1+y2=﹣2yH=﹣4,从而可求直线EF的斜率;
,从而可求抛物线C的方程;(Ⅱ)法一:根据当∠AHB的角平分线垂直x轴时,点H(4,2),可得kHE=﹣kHF , 设E(x1 , y1),F(x2 , y2),可得y1+y2=﹣2yH=﹣4,从而可求直线EF的斜率;
法二:求得直线HA的方程为 ![]() ,与抛物线方程联立,求出E,F的坐标,从而可求直线EF的斜率;(Ⅲ)法一:设A(x1 , y1),B(x2 , y2),求出直线HA的方程,直线HB的方程,从而可得直线AB的方程,令x=0,可得
,与抛物线方程联立,求出E,F的坐标,从而可求直线EF的斜率;(Ⅲ)法一:设A(x1 , y1),B(x2 , y2),求出直线HA的方程,直线HB的方程,从而可得直线AB的方程,令x=0,可得 ![]() ,再利用导数法,即可求得t的最小值.
,再利用导数法,即可求得t的最小值.
法二:求以H为圆心,HA为半径的圆方程,⊙M方程,两方程相减,可得直线AB的方程,当x=0时,直线AB在y轴上的截距 ![]() (m≥1),再利用导数法,即可求得t的最小值.
(m≥1),再利用导数法,即可求得t的最小值.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.

 学习实践园地系列答案
学习实践园地系列答案【题目】【2017河北唐山二模】某仪器经过检验合格才能出厂,初检合格率为![]() :若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为
:若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为![]() .每台仪器各项费用如表:
.每台仪器各项费用如表:
项目 | 生产成本 | 检验费/次 | 调试费 | 出厂价 |
金额(元) | 1000 | 100 | 200 | 3000 |
(Ⅰ)求每台仪器能出厂的概率;
(Ⅱ)求生产一台仪器所获得的利润为1600元的概率(注:利润![]() 出厂价
出厂价![]() 生产成本
生产成本![]() 检验费
检验费![]() 调试费);
调试费);
(Ⅲ)假设每台仪器是否合格相互独立,记![]() 为生产两台仪器所获得的利润,求
为生产两台仪器所获得的利润,求![]() 的分布列和数学期望.
的分布列和数学期望.