题目内容
【题目】已知三棱锥
的四个顶点都在球
的表面上，
平面
，
，
，
，
，则球的半径为______；若
是
的中点，过点作球的截面，则截面面积的最小值是______．
【答案】
【解析】
过底面外接圆的圆心
作垂直于底面的直线，则球心
在该直线上，可得
，然后即可求出球的半径，若
是
的中点，，重合，过点作球的截面，则截面面积最小时是与
垂直的面，即是三角形
的外接圆，然后算出答案即可.
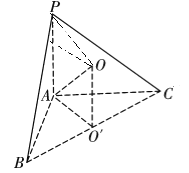
如图所示：由题意知底面三角形为直角三角形，所以底面外接圆的半径
，
过底面外接圆的圆心作垂直于底面的直线，则球心在该直线上，可得，
连接
，设外接球的半径为
，所以
，解得
．
若是的中点，，重合，过点
作球的截面，
则截面面积最小时是与垂直的面，即是三角形的外接圆，
而三角形的外接圆半径是斜边的一半，即2，所以截面面积为
．
故答案为：，
练习册系列答案
阅读快车系列答案
相关题目
【题目】某校从2011年到2018年参加“北约”“华约”考试而获得加分的学生（每位学生只能参加“北约”“华约”中的一种考试）人数可以通过以下表格反映出来.（为了方便计算，将2011年编号为1，2012年编号为2，依此类推）
年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
人数 | 2 | 3 | 4 | 4 | 7 | 7 | 6 | 6 |
（1）求这八年来，该校参加“北约”“华约”考试而获得加分的学生人数的中位数和方差；
（2）根据最近五年的数据，利用最小二乘法求出
与
之间的线性回归方程，并依此预测该校2019年参加“北约”“华约”考试而获得加分的学生人数.（结果要求四舍五入至个位）
参考公式：
.