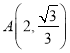题目内容
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]()
![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,
,![]() ,点
,点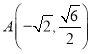 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)动直线l与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴的正半轴相交于点
轴的正半轴相交于点![]() ,
,![]() 为线段
为线段![]() 的中点,若
的中点,若![]() 为定值
为定值![]() ,请判断直线l是否过定点,求实数
,请判断直线l是否过定点,求实数![]() 的值,并说明理由.
的值,并说明理由.
【答案】(1)![]() ;(2)直线l过定点
;(2)直线l过定点![]() ,
,![]() ,理由见解析.
,理由见解析.
【解析】
(1)设点![]() 的坐标为
的坐标为![]() .由
.由![]() ,可得
,可得![]() ,
,![]() ,故椭圆
,故椭圆![]() 的标准方程为
的标准方程为![]() ,把点
,把点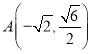 代入,求出
代入,求出![]() ,即得椭圆
,即得椭圆![]() 的标准方程;
的标准方程;
(2)由题意可设直线![]() 的方程为
的方程为![]()
![]() ,
,![]() ,则
,则![]() .由
.由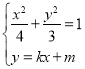 ,消去
,消去![]() ,韦达定理可得
,韦达定理可得![]() .由
.由![]() ,可得
,可得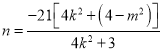 为定值,故
为定值,故![]() ,即求
,即求![]() ,即得直线l过定点.
,即得直线l过定点.
(1)设点![]() 的坐标为
的坐标为![]() .
.
由![]() ,
,![]() ,
,![]() ,
,![]() ,可得
,可得![]() ,
,![]() .
.
![]() 椭圆
椭圆![]() 的标准方程为
的标准方程为![]() ,
,![]() 点
点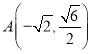 在椭圆
在椭圆![]() 上,
上,
![]() ,
,![]() ,
,
故椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由题意可知直线![]() 的斜率存在且不为0,设直线
的斜率存在且不为0,设直线![]() 的方程为
的方程为![]()
![]() ,
,
设![]() ,则
,则![]() .
.
由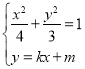 ,消去
,消去![]() ,整理可得
,整理可得![]() ,
,
则![]() ,
,![]() .
.
由![]() ,
,
可得![]() .
.
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]()
![]()
![]()
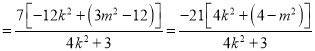 ,
,
若![]() 为定值,则必有
为定值,则必有![]() ,
,
解得![]() ,
,![]() ,
,![]() ,
,![]() .
.
故直线![]() 过定点
过定点![]() ,
,![]() .
.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目