题目内容

13．ABCD-A1B1C1D1为正方体，下列结论错误的是（　　）
A．BD∥平面CB1D1B．AC1⊥BDC．AC1⊥平面CB1D1D．AC1⊥BD1

分析 由题意画出图形，根据正方体的性质，结合线面平行、线面垂直的判断逐一核对四个选项得答案．

解答 解：如图，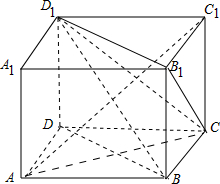

由ABCD-A1B1C1D1为正方体，可得BD∥B1D1，由线面平行的判定知，A正确；
由线面垂直的判断可知BD⊥面ACC1，由此可得AC1⊥BD，B正确；
由线面垂直的判定可得AC1⊥B1D1，AC1⊥B1C，
则由线面垂直的判定定理可得AC1⊥平面CB1D1，说明C正确；
由ABCD-A1B1C1D1为正方体，可得四边形ABC1D1为长方形，若AC1⊥BD1，
可得AB=BC1，矛盾，∴D错误．
故选：D．

点评 本题考查了棱柱的结构特征，考查了空间中的点线面的位置关系，考查了线面平行、线面垂直的判断和性质，是中档题．

练习册系列答案
相关题目
12．已知z∈C，满足不等式z$\overline{z}$+iz-i$\overline{z}$≤0的点Z的集合用阴影表示为（　　）
A．B．C．D．
13．若|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=$\sqrt{3}$，且$\overrightarrow{a}$与$\overrightarrow{b}$夹角为$\frac{π}{6}$，则|$\overrightarrow{a}$-$\overrightarrow{b}$|等于$\sqrt{3}$．
8．如图所示，在正方体ABCD-A1B1C1D1中，E为DD1上一点，且DE=$\frac{1}{3}$DD1，F是侧面CDD1C1上的动点，且B1F∥平面A1BE，则B1F与平面CDD1C1所成角的正切值构成的集合是（　　）
A．{$\frac{3}{2}$}B．{$\frac{2}{5}\sqrt{13}$}C．{m|$\frac{3}{2}$≤m≤$\frac{3}{2}$$\sqrt{2}$}D．{m|$\frac{2}{5}$$\sqrt{13}$≤m≤$\frac{3}{2}$}
18．过点M（2，4）与抛物线y2=8x只有一个公共点的直线共有（　　）
A．1B．2C．3D．4
5．已知抛物线y2=2x的焦点是F，准线是l，点M（2，m）是抛物线上一点，则经过点F、M且与l相切的圆的不同情况种数是（　　）
A．1种B．2种C．3种D．4种
2．若A（5，0）、B（-1，0）、C（-3，3）三点的外接圆为圆M，点D（m，3）在圆M上，求m的值．
3．设等差数列{an}的前n项和为Sn，已知a3=12，S12＞0，S13＜0．求Sn的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网