题目内容
8. 如图所示,在正方体ABCD-A1B1C1D1中,E为DD1上一点,且DE=$\frac{1}{3}$DD1,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则B1F与平面CDD1C1所成角的正切值构成的集合是( )
如图所示,在正方体ABCD-A1B1C1D1中,E为DD1上一点,且DE=$\frac{1}{3}$DD1,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则B1F与平面CDD1C1所成角的正切值构成的集合是( )| A. | {$\frac{3}{2}$} | B. | {$\frac{2}{5}\sqrt{13}$} | C. | {m|$\frac{3}{2}$≤m≤$\frac{3}{2}$$\sqrt{2}$} | D. | {m|$\frac{2}{5}$$\sqrt{13}$≤m≤$\frac{3}{2}$} |
分析 分别在CC1、C1D1上取点N、M,使得CN=$\frac{1}{3}$CC1,D1M=$\frac{1}{3}$D1C1,连接B1N、B1M,可证明平面MNB1∥平面A1BE,由B1F∥平面A1BE知点F在线段MN上,易证∠B1FC1为B1F与平面CDD1C1所成角,tan∠B1FC1=$\frac{{B}_{1}{C}_{1}}{{C}_{1}F}$,设出棱长,可求得C1F的最大值、最小值,从而可得答案.
解答 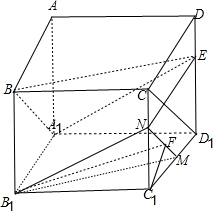 解:如图:分别在CC1、C1D1上取点N、M,
解:如图:分别在CC1、C1D1上取点N、M,
使得CN=$\frac{1}{3}$CC1,D1M=$\frac{1}{3}$D1C1,连接B1N、B1M,则MN∥CD1,
∵BC∥AD,BC=AD,AD∥A1D1,AD=A1D1,∴BC∥A1D1,BC=A1D1,
∴四边形BCD1A1为平行四边形,则CD1∥BA1,
∴MN∥BA1,
∵CN=$\frac{1}{3}$CC1,DE=$\frac{1}{3}$DD1,∴NE∥C1D1,NE=C1D1,
又C1D1∥A1B1,C1D1=A1B1,
∴NE∥A1B1,NE=A1B1,
∴四边形NEA1B1为平行四边形,则B1N∥A1E,
且MN∩B1N=N,
∴平面MNB1∥平面A1BE,
∵B1F∥平面A1BE,点F必在线段MN上,
连接C1F,∵B1C1⊥平面CDD1C1,∴∠B1FC1即为B1F与平面CDD1C1所成角,
设正方体棱长为3,则C1N=C1M=2,当F为MN中点时,C1F最短为$\sqrt{2}$,
当F与M或N重合时,C1F最长为2,
tan∠B1FC1=$\frac{{B}_{1}{C}_{1}}{{C}_{1}F}$∈[$\frac{3}{2}$,$\frac{3\sqrt{2}}{2}$],即所求正切值的取值范围是[$\frac{3}{2}$,$\frac{3\sqrt{2}}{2}$].
故选:C.
点评 本题考查直线与平面所成的角、面面平行的判定及性质,考查学生分析问题解决问题的能力及空间想象能力.

 阅读快车系列答案
阅读快车系列答案| A. | BD∥平面CB1D1 | B. | AC1⊥BD | C. | AC1⊥平面CB1D1 | D. | AC1⊥BD1 |