题目内容
19.设x,y满足约束条件$\left\{\begin{array}{l}3x-y-2≤0\\ x-y≥0\\ x≥0,y≥0\end{array}\right.$,若目标函数 $z=x+\frac{m}{2}y(m>0)$的最大值为2,则$y=sin(mx+\frac{π}{3})$的图象向右平移$\frac{π}{6}$后的表达式为( )| A. | $y=sin(2x+\frac{π}{6})$ | B. | $y=sin(x+\frac{π}{6})$ | C. | y=sin2x | D. | $y=sin(2x+\frac{2π}{3})$ |
分析 作出不等式组对应的平面区域,利用线性规划的知识求出m的值,利用三角函数的图象关系进行平移即可.
解答 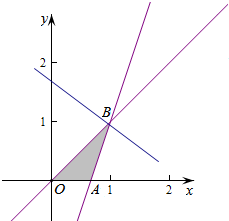 解:作出不等式组对应的平面区域如图,
解:作出不等式组对应的平面区域如图,
∵m>0,
∴平移直线$z=x+\frac{m}{2}y(m>0)$,
则由图象知,直线$z=x+\frac{m}{2}y(m>0)$经过点B时,直线截距最大,
此时z最大为2,
由$\left\{\begin{array}{l}{3x-y-2=0}\\{x-y=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,即B(1,1),
则1+$\frac{m}{2}$=2,
解得m=2,
则$y=sin(mx+\frac{π}{3})$=sin(2x+$\frac{π}{3}$),
则$y=sin(mx+\frac{π}{3})$的图象向右平移$\frac{π}{6}$后,
得到y=sin[2(x-$\frac{π}{6}$)+$\frac{π}{3}$]=sin2x,
故选:C.
点评 本题主要考查三角函数解析式的求解以及线性规划的应用,根据条件求出m的取值是解决本题的关键.

练习册系列答案
相关题目
14.设集合A={x|x2-2x-3<0},B={y|y=ex,x∈R},则A∩B=( )
| A. | (0,3) | B. | (0,2) | C. | (0,1) | D. | (1,2) |
4.已知A={x|x=3k-1,k∈Z},则下列表示正确的是( )
| A. | -1∉A | B. | -11∈A | C. | 3k+2∉A | D. | 3k2-1∈A |
11.设向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,3),若向量$\overrightarrow{a}-λ\overrightarrow{b}$与向量$\overrightarrow{c}$=(-5,-6)共线,则λ的值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{4}{13}$ | C. | $-\frac{4}{9}$ | D. | 4 |
8.市积极倡导学生参与绿色环保活动,其中代号为“环保卫士--12369”的绿色环保活动小组对2014年1月-2014年12月(一月)内空气质量指数API进行监测,如表是在这一年随机抽取的100天的统计结果:
(Ⅰ)若市某企业每天由空气污染造成的经济损失P(单位:元)与空气质量指数API(记为t)的关系为:$P=\left\{\begin{array}{l}0,0≤t≤100\\ 4t-400,100<t≤300\\ 1500,t>300\end{array}\right.$,在这一年内随机抽取一天,估计该天经济损失P∈(200,600]元的概率;
(Ⅱ)若本次抽取的样本数据有30天是在供暖季节,其中有8天为重度污染,完成2×2列联表,并判断是否有95%的把握认为A市本年度空气重度污染与供暖有关?
下面临界值表功参考.
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
| 指数API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(Ⅱ)若本次抽取的样本数据有30天是在供暖季节,其中有8天为重度污染,完成2×2列联表,并判断是否有95%的把握认为A市本年度空气重度污染与供暖有关?
| 非重度污染 | 重度污染 | 合计 | |
| 供暖季 | 22 | 8 | 30 |
| 非供暖季 | 63 | 7 | 70 |
| 合计 | 85 | 15 | 100 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
 如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥底面ABCD,E、F分别为AB、PC的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥底面ABCD,E、F分别为AB、PC的中点.