题目内容
12.过点P(1,$\sqrt{3}$)作圆x2+y2=1的两条切线,切点分别为A,B,则$\overrightarrow{PA}•\overrightarrow{PB}$=$\frac{3}{2}$.分析 根据直线与圆相切的性质可求PA=PB,及∠APB,然后代入向量数量积的定义可求$\overrightarrow{PA}•\overrightarrow{PB}$.
解答 解:连接OA,OB,PO
则OA=OB=1,PO=,2,OA⊥PA,OB⊥PB,
Rt△PAO中,OA=1,PO=2,PA=$\sqrt{3}$
∴∠OPA=30°,∠BPA=2∠OPA=60°
∴$\overrightarrow{PA}•\overrightarrow{PB}$=$|\overrightarrow{PA}|•|\overrightarrow{PB}|cos60°$=$\sqrt{3}×\sqrt{3}×\frac{1}{2}$=$\frac{3}{2}$
故答案为:$\frac{3}{2}$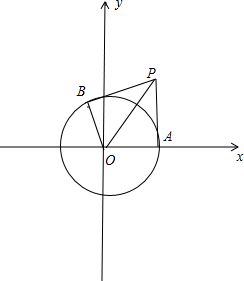
点评 本题主要考查了圆的切线性质的应用及平面向量的数量积的定义的应用,属于基础试题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
7.在区间[0,2]上随机地取一个数x,则事件“-1≤log${\;}_{\frac{1}{2}}$(x+$\frac{1}{2}$)≤1”发生的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
17.若复数z满足$\frac{\overline{z}}{1-i}$=i,其中i为虚数单位,则z=( )
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
2.若a为实数,且(2+ai)(a-2i)=-4i,则a=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
