题目内容
17.若复数z满足$\frac{\overline{z}}{1-i}$=i,其中i为虚数单位,则z=( )| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
分析 直接利用复数的乘除运算法则化简求解即可.
解答 解:$\frac{\overline{z}}{1-i}$=i,则$\overline{z}$=i(1-i)=1+i,
可得z=1-i.
故选:A.
点评 本题考查复数的基本运算,基本知识的考查.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
7.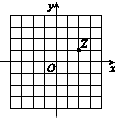 若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,则复数$\frac{z}{1-2i}$的共轭复数是( )
若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,则复数$\frac{z}{1-2i}$的共轭复数是( )
 若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,则复数$\frac{z}{1-2i}$的共轭复数是( )
若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,则复数$\frac{z}{1-2i}$的共轭复数是( )| A. | -$\frac{3}{5}$i | B. | -i | C. | $\frac{3}{5}$i | D. | i |
5.要得到函数y=sin(4x-$\frac{π}{3}$)的图象,只需要将函数y=sin4x的图象( )个单位.
| A. | 向左平移$\frac{π}{12}$ | B. | 向右平移$\frac{π}{12}$ | C. | 向左平移$\frac{π}{3}$ | D. | 向右平移$\frac{π}{3}$ |
2.一条光线从点(-2,-3)射出,经y轴反射后与圆(x+3)2+(y-2)2=1相切,则反射光线所在直线的斜率为( )
| A. | -$\frac{5}{3}$或-$\frac{3}{5}$ | B. | -$\frac{3}{2}$或-$\frac{2}{3}$ | C. | -$\frac{5}{4}$或-$\frac{4}{5}$ | D. | -$\frac{4}{3}$或-$\frac{3}{4}$ |
9.过双曲线x2-$\frac{{y}^{2}}{3}$=1的右焦点且与x轴垂直的直线,交该双曲线的两条渐近线于A、B两点,则|AB|=( )
| A. | $\frac{4\sqrt{3}}{3}$ | B. | 2$\sqrt{3}$ | C. | 6 | D. | 4$\sqrt{3}$ |
7.设全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},则A∩(∁UB)=( )
| A. | {1,2,5,6} | B. | {1} | C. | {2} | D. | {1,2,3,4} |