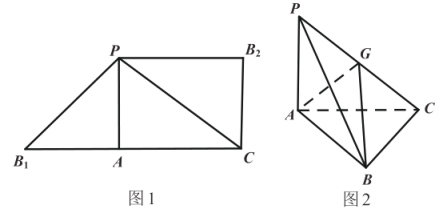
ЬтФПФкШн
ЁОЬтФПЁПИїЯюЮЊе§Ъ§ЕФЪ§Са![]() ШчЙћТњзуЃКДцдкЪЕЪ§
ШчЙћТњзуЃКДцдкЪЕЪ§![]() ЃЌЖдШЮвте§ећЪ§nЃЌ
ЃЌЖдШЮвте§ећЪ§nЃЌ![]() КуГЩСЂЃЌЧвДцдке§ећЪ§nЃЌЪЙЕУ
КуГЩСЂЃЌЧвДцдке§ећЪ§nЃЌЪЙЕУ![]() Лђ
Лђ![]() ГЩСЂЃЌдђГЦЪ§Са
ГЩСЂЃЌдђГЦЪ§Са![]() ЮЊЁАНєУмЪ§СаЁБЃЌkГЦЮЊЁАНєУмЪ§СаЁБ
ЮЊЁАНєУмЪ§СаЁБЃЌkГЦЮЊЁАНєУмЪ§СаЁБ![]() ЕФЁАНєУмЖШЁБЃЎвбжЊЪ§Са
ЕФЁАНєУмЖШЁБЃЎвбжЊЪ§Са![]() ЕФИїЯюЮЊе§Ъ§ЃЌЧАnЯюКЭЮЊ
ЕФИїЯюЮЊе§Ъ§ЃЌЧАnЯюКЭЮЊ![]() ЃЌЧвЖдШЮвте§ећЪ§nЃЌ
ЃЌЧвЖдШЮвте§ећЪ§nЃЌ![]() ЃЈAЃЌBЃЌCЮЊГЃЪ§ЃЉКуГЩСЂЃЎ
ЃЈAЃЌBЃЌCЮЊГЃЪ§ЃЉКуГЩСЂЃЎ
ЃЈ1ЃЉЕБ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪБЃЌ
ЪБЃЌ
ЂйЧѓЪ§Са![]() ЕФЭЈЯюЙЋЪНЃЛ
ЕФЭЈЯюЙЋЪНЃЛ
ЂкжЄУїЪ§Са![]() ЪЧЁАНєУмЖШЁБЮЊ3ЕФЁАНєУмЪ§СаЁБЃЛ
ЪЧЁАНєУмЖШЁБЮЊ3ЕФЁАНєУмЪ§СаЁБЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌвбжЊЪ§Са
ЪБЃЌвбжЊЪ§Са![]() КЭЪ§Са
КЭЪ§Са![]() ЖМЮЊЁАНєУмЪ§СаЁБЃЌЁАНєУмЖШЁБЗжБ№ЮЊ
ЖМЮЊЁАНєУмЪ§СаЁБЃЌЁАНєУмЖШЁБЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌЧѓЪЕЪ§BЕФШЁжЕЗЖЮЇЃЎ
ЃЌЧѓЪЕЪ§BЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй![]() ЂкМћНтЮіЃЛЃЈ2ЃЉ
ЂкМћНтЮіЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЙЋЪН![]() ЕУЕН
ЕУЕН![]() ЪЧвдЪзЯюЮЊ1ЃЌЙЋВюЮЊ2ЕФЕШВюЪ§СаЃЌЕУЕНЭЈЯюЙЋЪНЃЛМЦЫу
ЪЧвдЪзЯюЮЊ1ЃЌЙЋВюЮЊ2ЕФЕШВюЪ§СаЃЌЕУЕНЭЈЯюЙЋЪНЃЛМЦЫу![]() КуГЩСЂЃЌЕУЕНжЄУї.
КуГЩСЂЃЌЕУЕНжЄУї.
ЃЈ2ЃЉИљОнЕнЭЦЙЋЪНЕУЕН![]() ЪЧвдЪзЯю
ЪЧвдЪзЯю![]() ЃЌЙЋБШ
ЃЌЙЋБШ![]() ЕФЕШБШЪ§СаЃЌПМТЧ
ЕФЕШБШЪ§СаЃЌПМТЧ![]() КЭ
КЭ![]() СНжжЧщПіЃЌМЦЫуЕУЕН
СНжжЧщПіЃЌМЦЫуЕУЕН![]() ЃЌИљОн
ЃЌИљОн![]() НтЕУД№АИ.
НтЕУД№АИ.
ЃЈ1ЃЉЂйЕБ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
ЯрМѕЕУЃК![]() ЃЌ
ЃЌ
ећРэЕУЃК![]() ЃЌвђЮЊ
ЃЌвђЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
МДга![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЎ
ЃЎ
дђ![]() ЪЧвдЪзЯюЮЊ1ЃЌЙЋВюЮЊ2ЕФЕШВюЪ§СаЃЌдђ
ЪЧвдЪзЯюЮЊ1ЃЌЙЋВюЮЊ2ЕФЕШВюЪ§СаЃЌдђ![]() ЃЎ
ЃЎ
Ђк![]() ЃЌЕУ
ЃЌЕУ![]() ЫцзХ
ЫцзХ![]() ЕФдіДѓЖјМѕаЁЃЌ
ЕФдіДѓЖјМѕаЁЃЌ
дђЖдШЮвте§ећЪ§nЃЌ![]() КуГЩСЂЃЌЧвДцдк
КуГЩСЂЃЌЧвДцдк![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЎ
ЃЎ
дђЪ§Са![]() ЪЧЁАНєУмЖШЁБ3ЕФЁАНєУмЪ§СаЁБЃЎ
ЪЧЁАНєУмЖШЁБ3ЕФЁАНєУмЪ§СаЁБЃЎ
ЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЯрМѕЕУЃК
ЃЌЯрМѕЕУЃК![]() ЃЌ
ЃЌ
Шє![]() ЃЌдђЩЯЪНгвЖЫжа
ЃЌдђЩЯЪНгвЖЫжа![]() ЃЌгы
ЃЌгы![]() УЌЖмЃЛ
УЌЖмЃЛ
Шє![]() ЃЌдђЩЯЪНзѓЖЫ
ЃЌдђЩЯЪНзѓЖЫ![]() ЃЌгы
ЃЌгы![]() УЌЖмЃЌдђ
УЌЖмЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
дђ![]() ЮЊГЃЪ§ЃЌМД
ЮЊГЃЪ§ЃЌМД![]() ЪЧвдЪзЯю
ЪЧвдЪзЯю![]() ЃЌЙЋБШ
ЃЌЙЋБШ![]() ЕФЕШБШЪ§СаЃЎ
ЕФЕШБШЪ§СаЃЎ
вђЮЊЪ§Са![]() ЮЊЁАНєУмЪ§СаЁБЃЌдђ
ЮЊЁАНєУмЪ§СаЁБЃЌдђ![]() ЃЌ Ыљвд
ЃЌ Ыљвд![]() ЃЌгж
ЃЌгж![]() ЃЎ
ЃЎ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЖдШЮвте§ећЪ§
ЃЌЖдШЮвте§ећЪ§![]() КуГЩСЂЃЌ
КуГЩСЂЃЌ
ЧвДцдке§ећЪ§![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌЫљвдЪ§Са
ЃЌЫљвдЪ§Са![]() ЕФЁАНєУмЖШЁБЮЊ
ЕФЁАНєУмЖШЁБЮЊ![]() ЃЌ
ЃЌ
гж![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ДЫЪБ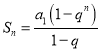 ЃЌ
ЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјМѕаЁЃЌ
ЕФдіДѓЖјМѕаЁЃЌ
Ыљвд![]() ЃЌЖдШЮвте§ећЪ§
ЃЌЖдШЮвте§ећЪ§![]() КуГЩСЂЃЌ
КуГЩСЂЃЌ
ЧвЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЫљвдЪ§Са
ЃЌЫљвдЪ§Са![]() ЕФЁАНєУмЖШЁБЮЊ
ЕФЁАНєУмЖШЁБЮЊ![]() ЃЌ
ЃЌ
дђ![]() ЃЌгы
ЃЌгы![]() УЌЖмЃЌВЛГЩСЂЃЛ
УЌЖмЃЌВЛГЩСЂЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЖдШЮвте§ећЪ§
ЃЌЖдШЮвте§ећЪ§![]() КуГЩСЂЃЌ
КуГЩСЂЃЌ
ЧвДцдке§ећЪ§![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌ
ЃЌ
дђДЫЪБ![]() ЕФЁАНєУмЖШЁБЮЊ
ЕФЁАНєУмЖШЁБЮЊ![]() ЃЌМД
ЃЌМД![]() ЃЎ
ЃЎ
Жј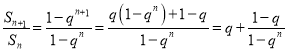 ЫцзХ
ЫцзХ![]() ЕФдіДѓЖјМѕаЁЃЌ
ЕФдіДѓЖјМѕаЁЃЌ
дђ![]() ЖдШЮвте§ећЪ§
ЖдШЮвте§ећЪ§![]() КуГЩСЂЃЌ
КуГЩСЂЃЌ
ЧвЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФЁАНєУмЖШЁБ
ЕФЁАНєУмЖШЁБ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ЙЪ![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃКЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ![]() ЃЎ
ЃЎ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИЁОЬтФПЁПФГЙЋЫОЮЊСЫЖдФГжжЩЬЦЗНјааКЯРэЖЈМлЃЌашСЫНтИУЩЬЦЗЕФдТЯњЪлСП![]() ЃЈЕЅЮЛЃКЭђМўЃЉгыдТЯњЪлЕЅМл
ЃЈЕЅЮЛЃКЭђМўЃЉгыдТЯњЪлЕЅМл![]() ЃЈЕЅЮЛЃКдЊ/МўЃЉжЎМфЕФЙиЯЕЃЌЖдНќ
ЃЈЕЅЮЛЃКдЊ/МўЃЉжЎМфЕФЙиЯЕЃЌЖдНќ![]() ИідТЕФдТЯњЪлСП
ИідТЕФдТЯњЪлСП![]() КЭдТЯњЪлЕЅМл
КЭдТЯњЪлЕЅМл![]()
![]() Ъ§ОнНјааСЫЭГМЦЗжЮіЃЌЕУЕНвЛзщМьВтЪ§ОнШчБэЫљЪОЃК
Ъ§ОнНјааСЫЭГМЦЗжЮіЃЌЕУЕНвЛзщМьВтЪ§ОнШчБэЫљЪОЃК
дТЯњЪлЕЅМл |
|
|
|
|
|
|
дТЯњЪлСП |
|
|
|
|
|
|
ЃЈ1ЃЉШєгУЯпадЛиЙщФЃаЭФтКЯ![]() гы
гы![]() жЎМфЕФЙиЯЕЃЌЯжгаМзЁЂввЁЂБћШ§ЮЛЪЕЯАдБЙЄЧѓЕУЛиЙщжБЯпЗНГЬЗжБ№ЮЊЃК
жЎМфЕФЙиЯЕЃЌЯжгаМзЁЂввЁЂБћШ§ЮЛЪЕЯАдБЙЄЧѓЕУЛиЙщжБЯпЗНГЬЗжБ№ЮЊЃК![]() ЃЌ
ЃЌ![]() КЭ
КЭ![]() ЃЌЦфжагаЧвНігавЛЮЛЪЕЯАдБЙЄЕФМЦЫуНсЙћЪЧе§ШЗЕФЃЎЧыНсКЯЭГМЦбЇЕФЯрЙижЊЪЖЃЌХаЖЯФФЮЛЪЕЯАдБЙЄЕФМЦЫуНсЙћЪЧе§ШЗЕФЃЌВЂЫЕУїРэгЩЃЛ
ЃЌЦфжагаЧвНігавЛЮЛЪЕЯАдБЙЄЕФМЦЫуНсЙћЪЧе§ШЗЕФЃЎЧыНсКЯЭГМЦбЇЕФЯрЙижЊЪЖЃЌХаЖЯФФЮЛЪЕЯАдБЙЄЕФМЦЫуНсЙћЪЧе§ШЗЕФЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєгУ![]() ФЃаЭФтКЯ
ФЃаЭФтКЯ![]() гы
гы![]() жЎМфЕФЙиЯЕЃЌПЩЕУЛиЙщЗНГЬЮЊ
жЎМфЕФЙиЯЕЃЌПЩЕУЛиЙщЗНГЬЮЊ![]() ЃЌОМЦЫуИУФЃаЭКЭЃЈ1ЃЉжае§ШЗЕФЯпадЛиЙщФЃаЭЕФЯрЙижИЪ§
ЃЌОМЦЫуИУФЃаЭКЭЃЈ1ЃЉжае§ШЗЕФЯпадЛиЙщФЃаЭЕФЯрЙижИЪ§![]() ЗжБ№ЮЊ
ЗжБ№ЮЊ![]() КЭ
КЭ![]() ЃЌЧыгУ
ЃЌЧыгУ![]() ЫЕУїФФИіЛиЙщФЃаЭЕФФтКЯаЇЙћИќКУЃЛ
ЫЕУїФФИіЛиЙщФЃаЭЕФФтКЯаЇЙћИќКУЃЛ
ЃЈ3ЃЉвбжЊИУЩЬЦЗЕФдТЯњЪлЖюЮЊ![]() ЃЈЕЅЮЛЃКЭђдЊЃЉЃЌРћгУЃЈ2ЃЉжаЕФНсЙћЛиД№ЮЪЬтЃКЕБдТЯњЪлЕЅМлЮЊКЮжЕЪБЃЌЩЬЦЗЕФдТЯњЪлЖюдЄБЈжЕзюДѓЃПЃЈОЋШЗЕН
ЃЈЕЅЮЛЃКЭђдЊЃЉЃЌРћгУЃЈ2ЃЉжаЕФНсЙћЛиД№ЮЪЬтЃКЕБдТЯњЪлЕЅМлЮЊКЮжЕЪБЃЌЩЬЦЗЕФдТЯњЪлЖюдЄБЈжЕзюДѓЃПЃЈОЋШЗЕН![]() ЃЉ
ЃЉ
ВЮПМЪ§ОнЃК![]() .
.