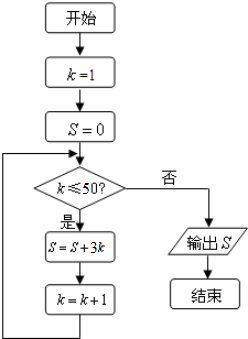
题目内容
12.已知0<a<1,则方程ax-|logax|=0的实根个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由ax-|logax|=0得ax=|logax|,作出两个函数y=ax与y=|logax|的图象,利用数形结合即可得到结论.
解答 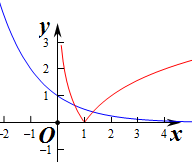 解:由ax-|logax|=0得ax=|logax|,
解:由ax-|logax|=0得ax=|logax|,
∵0<a<1,
∴作出两个函数y=ax与y=|logax|的图象如图:
由图象知,两个图象的交点个数为2个,
即方程ax-|logax|=0的实根个数为2个,
故选:B.
点评 本题主要考查方程根的个数的判断,根据函数和方程之间的关系转化为两个函数交点问题是解决本题的关键.

练习册系列答案
相关题目
2.某几何体的三视图如图所示,按图中所给的尺寸,该几何体的体积为( )
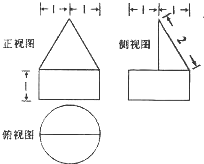

| A. | $\frac{\sqrt{3}π}{6}$+1 | B. | $\frac{\sqrt{3}π}{6}$+π | C. | $\frac{\sqrt{3}π}{3}$+π | D. | $\frac{\sqrt{3}π}{3}$+1 |
3.在空间中,设直线l的方向向量为$\overrightarrow{a}$,平面α的法向量为$\overrightarrow{b}$,对于原命题“若$\overrightarrow{a}$•$\overrightarrow{b}$=0,则l∥α”,下列判断正确的是( )
| A. | 原命题为真,否命题为真 | B. | 原命题为假,否命题为假 | ||
| C. | 原命题为假,否命题为真 | D. | 原命题为真,否命题为假 |
7.抛物线y2=4x的焦点为F,原点为O,直线AB经过点F且与抛物线交于A,B两点,抛物线的准线与x轴交于点C,若∠OFA=135°,则tan∠ACB=( )
| A. | 2$\sqrt{2}$ | B. | $\frac{4\sqrt{2}}{5}$ | C. | $\frac{4\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
4.抛物线x2=4y的焦点到准线的距离为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
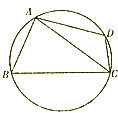 某棚户区改造工程规划用地近似为图中半径为R的圆面,图中圆内接四边形ABCD为拟定拆迁的棚户区,测得AB=AD=4百米,BC=6百米,CD=2百米.
某棚户区改造工程规划用地近似为图中半径为R的圆面,图中圆内接四边形ABCD为拟定拆迁的棚户区,测得AB=AD=4百米,BC=6百米,CD=2百米.