题目内容
【题目】已知命题p:x∈R,ax2+ax+1>0及命题q:x0∈R,x02﹣x0+a=0,若p∨q为真命题,p∧q为假命题,求实数a的取值范围.
【答案】解:命题p:x∈R,ax2+ax+1>0,当a=0时,1>0成立,因此a=0满足题意;当a≠0时,可得 ![]() ,解得0<a<4.
,解得0<a<4.
综上可得:0≤a<4.
命题q:x0∈R,x02﹣x0+a=0,∴△1=1﹣4a≥0,解得 ![]() .
.
∵p∨q为真命题,p∧q为假命题,
∴命题p与q必然一真一假.
∴ 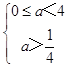 或
或 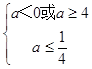 ,
,
解得a<0或 ![]() .
.
∴实数a的取值范围是a<0或 ![]()
【解析】题p:x∈R,ax2+ax+1>0,对a分类讨论:当a=0时,直接验证;当a≠0时,可得 ![]() .命题q:x0∈R,x02﹣x0+a=0,可得△1≥0.由p∨q为真命题,p∧q为假命题,可得命题p与q必然一真一假.解出即可.
.命题q:x0∈R,x02﹣x0+a=0,可得△1≥0.由p∨q为真命题,p∧q为假命题,可得命题p与q必然一真一假.解出即可.
【考点精析】关于本题考查的复合命题的真假,需要了解“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真才能得出正确答案.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】东莞某家具生产厂家根据市场调查分析,决定调整新产品生产方案,准备每周(按40个工时计算)生产书桌、书柜、电脑椅共120张,且书桌至少生产20张.已知生产这些家具每张所需工时和每张产值如表:
家具名称 | 书桌 | 书柜 | 电脑椅 |
工 时 |
|
|
|
产值(千元) | 4 | 3 | 2 |
问每周应生产书桌、书柜、电脑椅各多少张,才能使产值最高?最高产值是多少?(以千元为单位)