Question

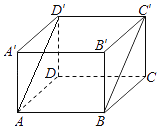
【题目】如图，长方体ABCD﹣A′B′C′D′中，AB=2 ，AD=2 ，AA′=2，

（Ⅰ）求异面直线BC′ 和AD所成的角；

（Ⅱ）求证：直线BC′∥平面ADD′A′．

Answer 1

【答案】(1) 异面直线BC′和AD所成的角为30°.

(2)证明见解析.

【解析】分析：（1）由AD∥BC，得∠CBC′是异面直线BC′和AD所成的角，由此能求出异面直线BC′和AD所成的角．（2）连结AD′，由AD′∥BC′，能证明直线BC′∥平面ADD′A′．

详解：（1）解：∵长方体ABCD﹣A′B′C′D′中，AD∥BC，∴∠CBC′是异面直线BC′和AD所成的角，

∵长方体ABCD﹣A′B′C′D′中，AB=2，AD=2 ，AA′=2，CC′⊥BC，

∴tan∠CBC′=，

∴∠CBC′=30°，

∴异面直线BC′和AD所成的角为30°

（2）解：证明：连结AD′，

∵长方体ABCD﹣A′B′C′D′中，AD′∥BC′，

又AD′平面ADD′A′，BC′平面ADD′A′，

∴直线BC′∥平面ADD′A′