题目内容
1.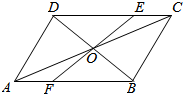 如图所示,已知O是?ABCD的中心,E,F分别在边CD,AB上,且$\frac{CE}{ED}=\frac{AF}{FB}$=$\frac{1}{2}$,你能用所学向量知识判断E,O,F三点是否在同一直线上吗?
如图所示,已知O是?ABCD的中心,E,F分别在边CD,AB上,且$\frac{CE}{ED}=\frac{AF}{FB}$=$\frac{1}{2}$,你能用所学向量知识判断E,O,F三点是否在同一直线上吗?
分析 由向量加法的几何意义及已知条件,便可得到$\overrightarrow{OE}=\overrightarrow{OC}+\frac{1}{3}\overrightarrow{CD}$,$\overrightarrow{FO}=\overrightarrow{AO}+\frac{1}{3}\overrightarrow{BA}$,可说明$\overrightarrow{OC}=\overrightarrow{AO},\overrightarrow{CD}=\overrightarrow{BA}$,从而得出$\overrightarrow{OE}=\overrightarrow{FO}$,这便说明E,O,F三点共线.
解答 解:根据条件及图形:$\overrightarrow{OE}=\overrightarrow{OC}+\overrightarrow{CE}$=$\overrightarrow{OC}+\frac{1}{3}\overrightarrow{CD}$,$\overrightarrow{FO}=\overrightarrow{FA}+\overrightarrow{AO}=\frac{1}{3}\overrightarrow{BA}+\overrightarrow{AO}$;
O是?ABCD的中心;
∴$\overrightarrow{AO}=\overrightarrow{OC}$,$\overrightarrow{BA}=\overrightarrow{CD}$;
∴$\overrightarrow{FO}=\overrightarrow{OE}$;
∴E,O,F三点共线.
点评 考查向量加法的几何意义,相等向量的定义,及共线向量基本定理.

练习册系列答案
相关题目
12. 设直线l过原点,其倾斜角为α,将直线l绕坐标原点沿逆时针方向旋转45°,得到直线l1,则直线l1的倾斜角为( )
设直线l过原点,其倾斜角为α,将直线l绕坐标原点沿逆时针方向旋转45°,得到直线l1,则直线l1的倾斜角为( )
 设直线l过原点,其倾斜角为α,将直线l绕坐标原点沿逆时针方向旋转45°,得到直线l1,则直线l1的倾斜角为( )
设直线l过原点,其倾斜角为α,将直线l绕坐标原点沿逆时针方向旋转45°,得到直线l1,则直线l1的倾斜角为( )| A. | α+45° | |
| B. | α-135° | |
| C. | 135°-α | |
| D. | 当0°≤α<135°时,为α+45°,当135°≤α<180°时,为α-135° |
16.二项式(x2-$\frac{2}{\sqrt{x}}$)5的展开式中常数项是( )
| A. | -32 | B. | 32 | C. | 80 | D. | -80 |