题目内容
11.已知命题p:方程ax2+ax-2=0在[-1,1]上只有一个解;命题q:只有一个实数x满足x2+2ax+2a≤0.若命题“p∨q”为假命题,求实数a的取值范围.分析 对方程a2x2+ax-2=0进行因式分解是解决该题的关键,得出方程的根(用a表示出).在[-1,1]上只有一个解,得出关于a的不等式,求出命题p为真的a的范围,利用x2+2ax+2a≤0相应的二次方程的判别式等于0得出关于a的方程,求出a,再根据“p或q”是假命题得出a的范围.
解答 解:由题意a≠0.
若p正确,a2x2+ax-2=(ax+2)(ax-1)=0的解为$\frac{1}{a}$或-$\frac{2}{a}$,
若方程在[-1,1]上有解,只需满足|$\frac{1}{a}$|≤1且|-$\frac{2}{a}$|>1,
解得a∈(-2,-1]∪[1,2),
故p错误时:a∈(-∞,-2]∪(-1,1)∪[2,+∞),
若q正确,即只有一个实数x满足x2+2ax+2a≤0,
则有△=4a2-8a=0,即a=0或2,
故q错误时,a∈(-∞,0)∪(0,2)∪(2,+∞)
若p或q是假命题,则p和q都是假命题,
综上所述:a∈(-∞,-2)∪(-1,0)∪(0,1)∪(2,+∞),
所以a的取值范围是:(-∞,-2)∪(-1,0)∪(0,1)∪(2,+∞)
点评 本题考查命题真假的判断,利用因式分解求出方程的根是解决本题的关键,再根据一元二次不等式与二次方程的关系转化相应的不等式问题,考查学生的等价转化思想,考查学生对复合命题真假的判断准则.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
2.1<|x|<2的解集是( )
| A. | -2<x<2 | B. | x<-1或x>1 | C. | -2<x<-1或1<x<2 | D. | -1<x<-2且1<x<2 |
6.函数y=$\left\{\begin{array}{l}{2x+3\\;x≤0}\\{x+3\\;0<x≤1}\\{5-x\\;x>1}\end{array}\right.$的值域为(-∞,4].
1.在极坐标系中,已知点P(ρ0,θ0),曲线F(ρ,θ)=0,则等式F(ρ0,θ0)=0成立是点P(ρ0,θ0)在曲线F(ρ,θ)=0上的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
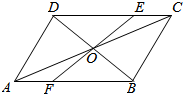 如图所示,已知O是?ABCD的中心,E,F分别在边CD,AB上,且$\frac{CE}{ED}=\frac{AF}{FB}$=$\frac{1}{2}$,你能用所学向量知识判断E,O,F三点是否在同一直线上吗?
如图所示,已知O是?ABCD的中心,E,F分别在边CD,AB上,且$\frac{CE}{ED}=\frac{AF}{FB}$=$\frac{1}{2}$,你能用所学向量知识判断E,O,F三点是否在同一直线上吗?