题目内容
13.设f(x)=$\left\{\begin{array}{l}{(x+1)^{2}\\;当x≤1}\\{\frac{1}{1-x}\\;当x>1}\end{array}\right.$,则f(f(x))=$\left\{\begin{array}{l}{({x}^{2}+2x+2)^{2},x≤1}\\{\frac{x-1}{x},x>1}\end{array}\right.$.分析 利用分段函数,代入计算,即可得出结论.
解答 解:x≤1时,f(x)=(x+1)2,f(f(x))=(x2+2x+2)2,
x>1时,f(x)=$\frac{1}{1-x}$,f(f(x))=$\frac{x-1}{x}$,
∴f(x)=$\left\{\begin{array}{l}{({x}^{2}+2x+2)^{2},x≤1}\\{\frac{x-1}{x},x>1}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{({x}^{2}+2x+2)^{2},x≤1}\\{\frac{x-1}{x},x>1}\end{array}\right.$.
点评 本题考查函数解析式,考查学生的计算能力,属于中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
8.如图,△ABC中,D,E分别为AB,AC的中点,CD与BE交于F,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}$=m$\overrightarrow{a}$+n$\overrightarrow{b}$,则m+n=( )
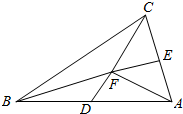

| A. | 1 | B. | $\frac{4}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
2.1<|x|<2的解集是( )
| A. | -2<x<2 | B. | x<-1或x>1 | C. | -2<x<-1或1<x<2 | D. | -1<x<-2且1<x<2 |
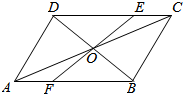 如图所示,已知O是?ABCD的中心,E,F分别在边CD,AB上,且$\frac{CE}{ED}=\frac{AF}{FB}$=$\frac{1}{2}$,你能用所学向量知识判断E,O,F三点是否在同一直线上吗?
如图所示,已知O是?ABCD的中心,E,F分别在边CD,AB上,且$\frac{CE}{ED}=\frac{AF}{FB}$=$\frac{1}{2}$,你能用所学向量知识判断E,O,F三点是否在同一直线上吗?