题目内容
10.已知x,y,z为正实数,且x2+y2+z2=2.则t=$\sqrt{5}$xy+yz的最大值是$\sqrt{6}$,此时(x,y,z)=($\frac{\sqrt{30}}{6}$,1,$\frac{\sqrt{6}}{6}$).分析 2=x2+y2+z2=(x2+$\frac{5}{6}$y2)+($\frac{1}{6}$y2+z2),利用基本不等式,即可求出$\sqrt{5}$xy+yz的最大值.
解答 解:因为2=x2+y2+z2=(x2+$\frac{5}{6}$y2)+($\frac{1}{6}$y2+z2)
≥2$\sqrt{\frac{5}{6}}$xy+2$\sqrt{\frac{1}{6}}$yz=$\frac{\sqrt{6}}{3}$($\sqrt{5}$xy+yz),
所以$\sqrt{5}$xy+yz≤$\sqrt{6}$,
故$\sqrt{5}$xy+yz的最大值为$\sqrt{6}$.此时x=$\frac{\sqrt{30}}{6}$,y=1,z=$\frac{\sqrt{6}}{6}$.
故答案为:$\sqrt{6}$,($\frac{\sqrt{30}}{6}$,1,$\frac{\sqrt{6}}{6}$).
点评 本题考查基本不等式的运用,考查学生的计算能力,2=x2+y2+z2=(x2+$\frac{5}{6}$y2)+($\frac{1}{6}$y2+z2)是解题的关键.

练习册系列答案
相关题目
2.1<|x|<2的解集是( )
| A. | -2<x<2 | B. | x<-1或x>1 | C. | -2<x<-1或1<x<2 | D. | -1<x<-2且1<x<2 |
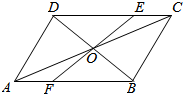 如图所示,已知O是?ABCD的中心,E,F分别在边CD,AB上,且$\frac{CE}{ED}=\frac{AF}{FB}$=$\frac{1}{2}$,你能用所学向量知识判断E,O,F三点是否在同一直线上吗?
如图所示,已知O是?ABCD的中心,E,F分别在边CD,AB上,且$\frac{CE}{ED}=\frac{AF}{FB}$=$\frac{1}{2}$,你能用所学向量知识判断E,O,F三点是否在同一直线上吗?