题目内容
【题目】当x∈[﹣2,1]时,不等式ax3﹣x2+4x+3≥0恒成立,则实数a的取值范围是( )
A.[﹣5,﹣3]
B.[﹣6,﹣ ![]() ]
]
C.[﹣6,﹣2]
D.[﹣4,﹣3]
【答案】C
【解析】解:当x=0时,不等式ax3﹣x2+4x+3≥0对任意a∈R恒成立; 当0<x≤1时,ax3﹣x2+4x+3≥0可化为a≥ ![]() ,
,
令f(x)= ![]() ,则f′(x)=
,则f′(x)= ![]() =﹣
=﹣ ![]() (*),
(*),
当0<x≤1时,f′(x)>0,f(x)在(0,1]上单调递增,
f(x)max=f(1)=﹣6,∴a≥﹣6;
当﹣2≤x<0时,ax3﹣x2+4x+3≥0可化为a≤ ![]() ,
,
由(*)式可知,当﹣2≤x<﹣1时,f′(x)<0,f(x)单调递减,当﹣1<x<0时,f′(x)>0,f(x)单调递增,
f(x)min=f(﹣1)=﹣2,∴a≤﹣2;
综上所述,实数a的取值范围是﹣6≤a≤﹣2,即实数a的取值范围是[﹣6,﹣2].
故选:C.
分x=0,0<x≤1,﹣2≤x<0三种情况进行讨论,分离出参数a后转化为函数求最值即可,利用导数即可求得函数最值,注意最后要对a取交集.

【题目】某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图.
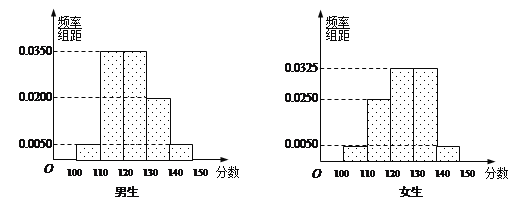
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
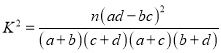 ,
,
【题目】某省的一个气象站观测点在连续4天里记录的![]() 指数
指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() (单位:
(单位: ![]() )的情况如表1:
)的情况如表1:

该省某市2016年11月![]() 指数频数分布如表2:
指数频数分布如表2:
|
|
|
|
|
|
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设![]() ,根据表1的数据,求出
,根据表1的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(附参考公式: ![]() ,其中
,其中 ,
, ![]() )
)
(2)小李在该市开了一家洗车店,经统计,洗车店平均每天的收入与![]() 指数由相关关系,如表3:
指数由相关关系,如表3:
|
|
|
|
|
|
日均收入(元) |
|
|
|
|
|
根据表3估计小李的洗车店该月份平均每天的收入.