题目内容
已知公差不为零的等差数列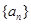 的前
的前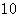 项和
项和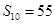 ,且
,且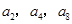 成等比数列.
成等比数列.
(Ⅰ)求数列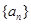 的通项公式;
的通项公式;
(Ⅱ)若数列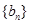 满足
满足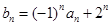 ,求
,求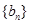 的前
的前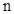 项和
项和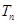 .
.
(Ⅰ)根据题意把等差数列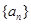 的前
的前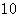 项和关系式和
项和关系式和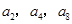 成等比数列的关系式都表示成首项
成等比数列的关系式都表示成首项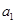 和公差
和公差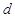 的方程式,解方程组即可得数列
的方程式,解方程组即可得数列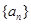 的通项公式;(Ⅱ)由(Ⅰ)中
的通项公式;(Ⅱ)由(Ⅰ)中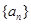 的通项公式易知数列
的通项公式易知数列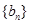 的通项公式,再对式中
的通项公式,再对式中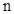 分奇数和偶数两种情况讨论,分别求和,即得结论.
分奇数和偶数两种情况讨论,分别求和,即得结论.
解析试题分析:(Ⅰ)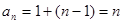 ;(Ⅱ)
;(Ⅱ) .
.
试题解析:(Ⅰ) 由已知得: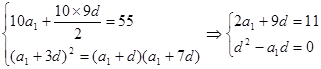
因为  所以
所以 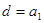 , 所以
, 所以 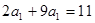 ,所以
,所以 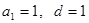
所以 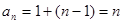 . 6分
. 6分
(Ⅱ) 
(ⅰ) 当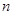 为奇数时,
为奇数时,
(ⅱ) 当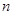 为偶数时,
为偶数时,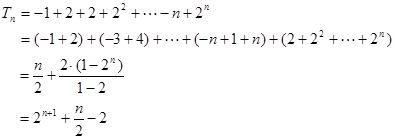 ,
,
所以 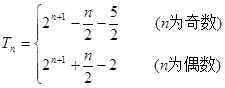 . 14分
. 14分
考点:1、等差数列的通项和前 项和公式;2、等比数列的性质;3、等比数列的前
项和公式;2、等比数列的性质;3、等比数列的前 项和公式.
项和公式.

练习册系列答案
相关题目
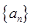 的前
的前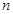 项和
项和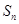 ,且满足
,且满足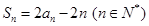 .
.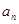 .
.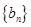 满足
满足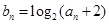 ,
,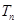 为数列{
为数列{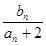 }的前
}的前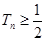 .
.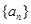 的各项均为正数,其前n项的和为
的各项均为正数,其前n项的和为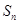 ,对于任意正整数m,n,
,对于任意正整数m,n, 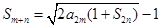 恒成立.
恒成立. 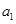 =1,求
=1,求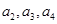 及数列
及数列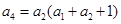 ,求证:数列
,求证:数列 }中,a1=1,
}中,a1=1, 是数列{
是数列{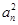 +p
+p 满足
满足 ,
, ,
, ,且
,且 是等比数列。
是等比数列。 的值;
的值; ;
; …
…
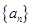 各项为非负实数,前n项和为
各项为非负实数,前n项和为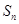 ,且
,且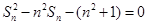
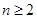 时,求
时,求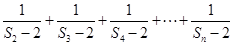 .
. 为公差不为
为公差不为 的等差数列,
的等差数列, 为前
为前 项和,
项和, 和
和 的等差中项为
的等差中项为 ,且
,且 .令
.令 数列
数列 的前
的前 .
. 及
及 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.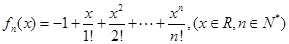
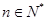 ,存在唯一的
,存在唯一的 ,满足
,满足 ;
;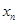 构成数列
构成数列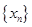 ,判断数列
,判断数列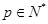 ,
,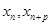 满足(Ⅰ),试比较
满足(Ⅰ),试比较 与
与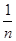 的大小.
的大小.