题目内容
13.下列说法:①如果非零向量$\overrightarrow{a}$与$\overrightarrow{b}$的方向相同或相反,那么$\overrightarrow{a}$+$\overrightarrow{b}$的方向必与$\overrightarrow{a}$,$\overrightarrow{b}$之一的方向相同;
②△ABC中,必有$\overrightarrow{AB}$$+\overrightarrow{BC}$+$\overrightarrow{CA}$=$\overrightarrow{0}$;
③若$\overrightarrow{AB}$+$\overrightarrow{BC}$$+\overrightarrow{CA}$=$\overrightarrow{0}$,则A,B,C为一个三角形的三个顶点;
④若$\overrightarrow{a}$,$\overrightarrow{b}$均为非零向量,则|$\overrightarrow{a}$+$\overrightarrow{b}$|与|$\overrightarrow{a}$|+|$\overrightarrow{b}$|一定相等.
其中正确说法的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 ①非零向量$\overrightarrow{a}$与$\overrightarrow{b}$的方向相同或相反时,$\overrightarrow{a}$+$\overrightarrow{b}$的方向与$\overrightarrow{a}$或$\overrightarrow{b}$的方向相同;
②△ABC中,$\overrightarrow{AB}$$+\overrightarrow{BC}$+$\overrightarrow{CA}$=$\overrightarrow{0}$;
③$\overrightarrow{AB}$+$\overrightarrow{BC}$$+\overrightarrow{CA}$=$\overrightarrow{0}$时,A,B,C三点不一定构成三角形;
④$\overrightarrow{a}$,$\overrightarrow{b}$均为非零向量时,|$\overrightarrow{a}$+$\overrightarrow{b}$|与|$\overrightarrow{a}$|+|$\overrightarrow{b}$|不一定相等.
解答 解:对于①,当非零向量$\overrightarrow{a}$与$\overrightarrow{b}$的方向相同或相反时,$\overrightarrow{a}$+$\overrightarrow{b}$的方向与$\overrightarrow{a}$或$\overrightarrow{b}$的方向相同,∴命题正确;
对于②,△ABC中,$\overrightarrow{AB}$$+\overrightarrow{BC}$+$\overrightarrow{CA}$=$\overrightarrow{0}$,∴命题正确;
对于③,当$\overrightarrow{AB}$+$\overrightarrow{BC}$$+\overrightarrow{CA}$=$\overrightarrow{0}$时,A,B,C不一定是一个三角形的三个顶点,如A、B、C三点共线时,∴命题错误;
对于④,当$\overrightarrow{a}$,$\overrightarrow{b}$均为非零向量时,|$\overrightarrow{a}$+$\overrightarrow{b}$|与|$\overrightarrow{a}$|+|$\overrightarrow{b}$|不一定相等,如$\overrightarrow{a}$、$\overrightarrow{b}$不共线时,∴命题错误.
综上,以上正确命题的个数为2.
故选:C.
点评 本题考查了平面向量的概念与应用问题,是基础题目.


| A. |  | B. |  | C. |  | D. |  |
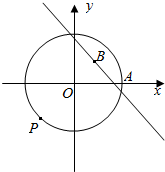 点A(2,0)是圆x2+y2=4上的定点,点B(1,1)是圆内一点,P为圆上的动点.
点A(2,0)是圆x2+y2=4上的定点,点B(1,1)是圆内一点,P为圆上的动点.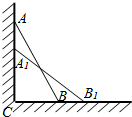 如图,一根木棒AB长为2米,斜靠在墙壁AC上,∠ABC=60°,若AB滑动至A1B1位置,且AA1=($\sqrt{3}$-$\sqrt{2}$)米,则AB中点D所经过的路程为$\frac{π}{12}$米.
如图,一根木棒AB长为2米,斜靠在墙壁AC上,∠ABC=60°,若AB滑动至A1B1位置,且AA1=($\sqrt{3}$-$\sqrt{2}$)米,则AB中点D所经过的路程为$\frac{π}{12}$米.