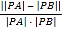题目内容
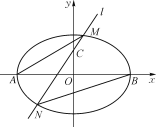
【题目】已知椭圆C:![]() (a>b>0)的左.右顶点分别为A,B,离心率为
(a>b>0)的左.右顶点分别为A,B,离心率为![]() ,点P
,点P![]() 为椭圆上一点.
为椭圆上一点.
(1) 求椭圆C的标准方程;
(2) 如图,过点C(0,1)且斜率大于1的直线l与椭圆交于M,N两点,记直线AM的斜率为k1,直线BN的斜率为k2,若k1=2k2,求直线l斜率的值.
【答案】(1)![]() +
+![]() =1;(2) k=
=1;(2) k=![]()
【解析】
(1)根据已知条件,建立方程组,求出a,b,即可得到椭圆的标准方程.
(2)设出直线l方程为y=kx+1,M(x1,y1),N(x2,y2),将直线l方程与椭圆方程联立,求出x1+x2和x1x2,根据条件求出k1和k2,代入k1=2k2化简计算,得到关于k的方程,解方程求出k的值.
(1)因为椭圆的离心率为![]() ,所以a=2c.
,所以a=2c.
又因为a2=b2+c2,所以b=![]() c.
c.
所以椭圆的标准方程为![]() +
+![]() =1.
=1.
又因为点P![]() 为椭圆上一点,所以
为椭圆上一点,所以![]() +
+![]() =1,解得c=1.
=1,解得c=1.
所以椭圆的标准方程为![]() +
+![]() =1.
=1.
(2)由椭圆的对称性可知直线l的斜率一定存在,设其方程为y=kx+1.
设M(x1,y1),N(x2,y2).
联立直线![]() 与椭圆的方程组
与椭圆的方程组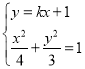 ,消去y可得(3+4k2)x2+8kx-8=0.
,消去y可得(3+4k2)x2+8kx-8=0.
所以由根与系数关系可知x1+x2=-![]() ,x1x2=-
,x1x2=-![]() .
.
因为k1=![]() ,k2=
,k2=![]() ,且k1=2k2,所以
,且k1=2k2,所以![]() =
=![]() .
.
即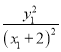 =
=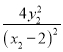 ,①
,①
又因为M(x1,y1),N(x2,y2)在椭圆上,
所以![]() .②
.②
将②代入①可得:![]() =
=![]() ,即3x1x2+10(x1+x2)+12=0.
,即3x1x2+10(x1+x2)+12=0.
所以3![]() +10
+10![]() +12=0,即12k2-20k+3=0.
+12=0,即12k2-20k+3=0.
解得k=![]() 或k=
或k=![]() ,又因为k>1,所以k=
,又因为k>1,所以k=![]() .
.

【题目】人们随着生活水平的提高,健康意识逐步加强,健身开始走进人们生活,在健身方面投入越来越多,为了调查参与健身的年轻人一年健身的花费情况,研究人员在![]() 地区随机抽取了参加健身的青年男性、女性各50名,将其花费统计情况如下表所示:
地区随机抽取了参加健身的青年男性、女性各50名,将其花费统计情况如下表所示:
分组(花费) | 频数 |
| 6 |
| 22 |
| 25 |
| 35 |
| 8 |
| 4 |
男性 | 女性 | 合计 | |
健身花费不超过2400元 | 23 | ||
健身花费超过2400元 | 20 | ||
合计 |
(1)完善二联表中的数据;
(2)根据表中的数据情况,判断是否有99%的把握认为健身的花费超过2400元与性别有关;
(3)求这100名被调查者一年健身的平均花费(同一组数据用该区间的中点值代替).
附:![]()
P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.01 |
k | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好