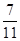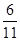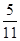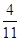题目内容

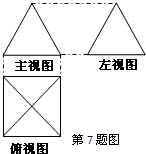
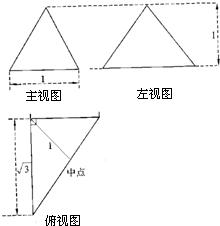
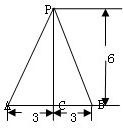
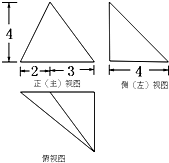
如图所示是三棱锥D-ABC的三视图，点O在三个视图中都是所在边的中点，则异面直线DO和AB所成角的余弦值等于（　　）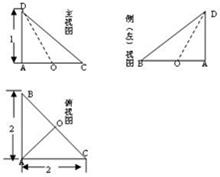
A．
3
3
B．
1
2
C．
3
D．
2
2
由题意得如图的直观图，从A出发的三个线段AB，AC，AD两两垂直且AB=AC=2，AD=1，O是中点，
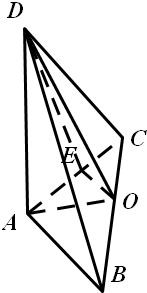
取AC中点E，连接OE，则OE=1，又可知AE=1，由于OE∥AB，，故角DOE即所求两异面直线所成的角
在直角三角形DAE中，求得DE=
2

由于O是中点，在直角三角形ABC中可以求得AO=
2

在直角三角形DAO中可以求得DO=
3

在三角形DOE中，由余弦定理得cos∠DOE=
1+3-2
2×1×
3
=
3
3

故选A
练习册系列答案
相关题目
已知一几何体的正视图与侧视图均为边长为2的正三角形，俯视图是半径为1的圆，则其表面积为（　　）
A．4πB．3πC．8πD．6π
如图，一个简单空间的三视图其主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形，则这个几何体的全面积是（　　）
A．12B．4+4
3
C．
4
2
3
D．
8
3
（2010•陕西高考理科•T7）若某空间几何体的三视图如图所示，则该几何体的体积是（　　）
A．
1
3
B．
2
3
C．1D．2
已知三棱锥的三视图如图所示，则它的外接球表面积为______．
一个几何体的三视图如图所示，其中正视图是一个边长为2的正三角形，俯视图是一正方形，那么该几何体的侧视图的面积为（　　）
A．1B．2C．
3
D．4
已知一个正三棱锥P-ABC的主视图如图所示，则此正三棱锥的侧面积等于（　　）
A．9
39
B．54C．27
5
D．36
3
某三棱锥的三视图如图所示，该三棱锥的体积为（　　）
A．80B．40C．
80
3
D．
40
3
已知空间4个球,它们的半径分别为2, 2, 3, 3,每个球都与其他三个球外切,另有一个小球与这4个球都外切,则这个小球的半径为（　　）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网