题目内容
15．在等差数列{an}中，其前n项和为Sn，若Sn =an2+（a+1）n+a+2，则an=-4n+1．分析 利用等差数列{an}中，其前n项和为Sn，Sn =an2+（a+1）n+a+2，求出a，再求an．
解答 解：∵等差数列{an}中，其前n项和为Sn，Sn =an2+（a+1）n+a+2，
∴a+2=0，
∴a=-2，
∴Sn =-2n2-n，
∴n≥2时，an=Sn-Sn-1=-4n+1．
n=1时，S1=-3，满足上式，
∴an=-4n+1．
故答案为：-4n+1．
点评 本题考查等差数列的通项与求和，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
3．已知函数f（x）=sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的图象关于直线x=$\frac{π}{3}$对称，且f（$\frac{π}{12}$）=0，则当ω取最小值时φ=（ ）
| A． | -$\frac{π}{3}$ | B． | -$\frac{π}{6}$ | C． | $\frac{π}{6}$ | D． | $\frac{π}{3}$ |
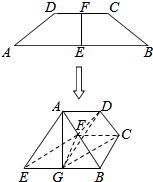在等腰梯形ABCD中，E，F分别是AB，CD的中点，AB=4，CD=2，AD=BC=$\sqrt{2}$，现将梯形AEFD沿EF折起，并记平面AEFD与平面BEFC所成二面角的平面角为θ，BE中点为G．