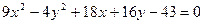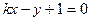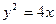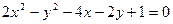题目内容
(1)原点O及直线
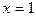 为曲线C的焦点和相应的准线;
为曲线C的焦点和相应的准线;(2)被直线
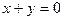 垂直平分的直线截曲线C所得的弦长恰好为
垂直平分的直线截曲线C所得的弦长恰好为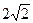 。
。若存在,求出曲线C的方程,若不存在,说明理由。
解:设存在符合题设的圆锥曲线C,此曲线离心率为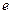 (
(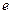 >0),P(x,y)是曲线C上任一点。
>0),P(x,y)是曲线C上任一点。
由圆锥曲线的定义有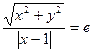
化简整理得,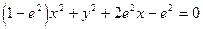 ①
①
设曲线C被直线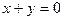 垂直平分,其弦长为
垂直平分,其弦长为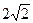 的弦所在直线方程为
的弦所在直线方程为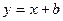 ,这弦的两个端点
,这弦的两个端点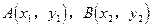
将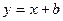 代入①式中,消去y得
代入①式中,消去y得
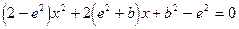 ②
②
由题意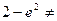 0,
0,
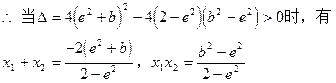
由此可解得AB的中点D的坐标为
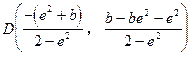
由条件(2),中点D在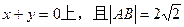 ,于是有:
,于是有:
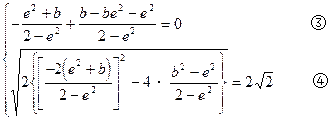
解③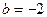 ,代入④得
,代入④得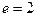 。
。
经检验符合题意,因此符合条件的曲线C存在,其方程为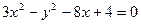 。
。
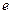 (
(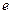 >0),P(x,y)是曲线C上任一点。
>0),P(x,y)是曲线C上任一点。由圆锥曲线的定义有
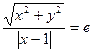
化简整理得,
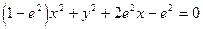 ①
①设曲线C被直线
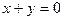 垂直平分,其弦长为
垂直平分,其弦长为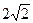 的弦所在直线方程为
的弦所在直线方程为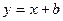 ,这弦的两个端点
,这弦的两个端点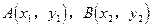
将
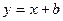 代入①式中,消去y得
代入①式中,消去y得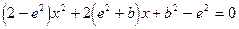 ②
②由题意
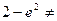 0,
0,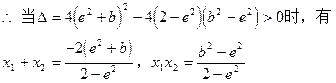
由此可解得AB的中点D的坐标为
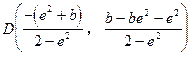
由条件(2),中点D在
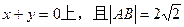 ,于是有:
,于是有: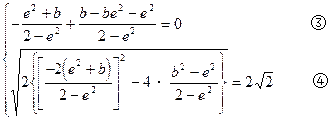
解③
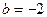 ,代入④得
,代入④得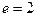 。
。经检验符合题意,因此符合条件的曲线C存在,其方程为
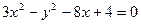 。
。这是一道开放性的题目,探求满足上述两个条件的圆锥曲线是否存在,本题的难点是题目没有具体的给出圆锥曲线的形状,由条件(1)给出焦点和相应的准线,因此可考虑用圆锥曲线统一定义,设离心率为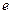 ,通过计算,推理,探求
,通过计算,推理,探求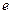 的存在性。
的存在性。
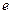 ,通过计算,推理,探求
,通过计算,推理,探求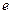 的存在性。
的存在性。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
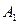 ,
,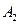 是一个圆一条直径的两个端点,
是一个圆一条直径的两个端点,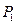
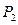 是与
是与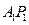 与
与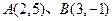 ,则线段AB的方程为( )
,则线段AB的方程为( )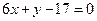
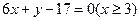
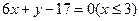
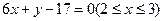


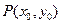 在椭圆
在椭圆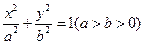 上,
上,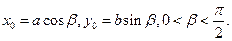 直线
直线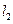 与直线
与直线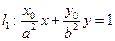 垂直,O为坐标原点,直线OP的倾斜角为
垂直,O为坐标原点,直线OP的倾斜角为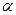 ,直线
,直线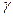 .
.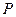 是椭圆
是椭圆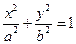 与直线
与直线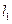 的唯一交点;
的唯一交点; 
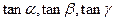 构成等比数列.
构成等比数列.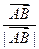 在向量
在向量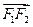 方向的投影是p,当(×)p2=1时,求直线l的方程;(Ⅲ)当(×)p2=m且满足2≤m≤4时,求DAOB面积的取值范围.
方向的投影是p,当(×)p2=1时,求直线l的方程;(Ⅲ)当(×)p2=m且满足2≤m≤4时,求DAOB面积的取值范围.