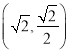题目内容
【题目】已知椭圆 ![]() 的离心率
的离心率 ![]() ,分别是椭圆的左、右顶点,点P是椭圆上的一点,直线PA、PB的倾斜角分别为α、β满足tanα+tanβ=1,则直线PA的斜率为
,分别是椭圆的左、右顶点,点P是椭圆上的一点,直线PA、PB的倾斜角分别为α、β满足tanα+tanβ=1,则直线PA的斜率为
【答案】![]()
【解析】解:由题意可知:A(﹣a,0),B(a,0),P(x,y),
椭圆的离心率e= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
整理得:a=2b,
∴椭圆方程为: ![]() ,
,
∴y2= ![]() ,则
,则 ![]() =﹣
=﹣ ![]() ,
,
直线PA、PB的倾斜角分别为α、β,
∴kPA=tanα= ![]() ,kPB=tanβ=
,kPB=tanβ= ![]() ,
,
∴tanαtanβ= ![]()
![]() =
= ![]() =﹣
=﹣ ![]() ,
,
直线PA、PB的倾斜角分别为α、β满足tanα+tanβ=1,
∴tanα,tanβ是方程x2﹣x﹣ ![]() =0的两个根,
=0的两个根,
解得:x= ![]() ,
,
∴直线PA的斜率kPA=tanα= ![]() ,
,
所以答案是: ![]() .
.

练习册系列答案
相关题目
【题目】某地区为了解70﹣80岁的老人的日平均睡眠时间(单位:h),随机选择了50位老人进行调查,下表是这50位老人睡眠时间的频率分布表:
序号i | 分组 | 组中值(Gi) | 频数 | 频率(Fi) |
1 | [4,5) | 4.5 | 6 | 0.12 |
2 | [5,6) | 5.5 | 10 | 0.20 |
3 | [6,7) | 6.5 | 20 | 0.40 |
4 | [7,8) | 7.5 | 10 | 0.20 |
5 | [8,9] | 8.5 | 4 | 0.08 |
在上述统计数据的分析中一部分计算见算法流程图,则输出的S的值为 .