题目内容
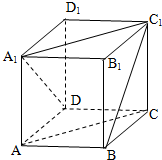 如图,正方体ABCD-A1B1C1D1,异面直线BC1、A1D所成的角的大小为
如图,正方体ABCD-A1B1C1D1,异面直线BC1、A1D所成的角的大小为考点:直线与平面所成的角,异面直线及其所成的角
专题:空间角
分析:由BC1∥AD1,AD1⊥A1D,能求出异面直线BC1、A1D所成的角的大小;利用AC∥A1C1,且A1C1=BC1=A1B,能求出异面直线BC1、AC所成的角的大小为60°;由C1C⊥平面ABCD,知∠C1BC是直线BC1与平面ABCD所成的角,由此能求出直线BC1与平面ABCD所成的角的大小;连接BD交AC于点O,连结C1O,∠BC1O是直线BC1与平面ACC1A1所成的角,由此能求出直线BC1与平面ACC1A1所成的角的大小.
解答:
解:∵BC1∥AD1,AD1⊥A1D,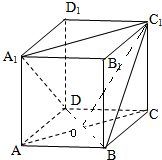
∴异面直线BC1、A1D所成的角的大小为90°;
∵AC∥A1C1,且A1C1=BC1=A1B,
∴异面直线BC1、AC所成的角的大小为60°;
∵C1C⊥平面ABCD,
∴∠C1BC是直线BC1与平面ABCD所成的角,
∵∠C1BC=45°,∴直线BC1与平面ABCD所成的角的大小为45°,
连接BD交AC于点O,连结C1O,
由已知得BO⊥平面ACC1A1,
∴∠BC1O是直线BC1与平面ACC1A1所成的角,
∵BO=
BC1,∴sin∠BC1O=
,
∴∠BC1O=30°,即直线BC1与平面ACC1A1所成的角为30°.
故答案为:90°;60°;45°,30°.

∴异面直线BC1、A1D所成的角的大小为90°;
∵AC∥A1C1,且A1C1=BC1=A1B,
∴异面直线BC1、AC所成的角的大小为60°;
∵C1C⊥平面ABCD,
∴∠C1BC是直线BC1与平面ABCD所成的角,
∵∠C1BC=45°,∴直线BC1与平面ABCD所成的角的大小为45°,
连接BD交AC于点O,连结C1O,
由已知得BO⊥平面ACC1A1,
∴∠BC1O是直线BC1与平面ACC1A1所成的角,
∵BO=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BC1O=30°,即直线BC1与平面ACC1A1所成的角为30°.
故答案为:90°;60°;45°,30°.
点评:本题考查空间角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
将抛物线y2=4x按向量
=(1,2)平移后与直线x-2y+m=0相切,则m的值为( )
| a |
| A、-1 | B、7 | C、9 | D、1 |
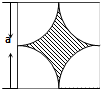 如图所示,墙上挂有边长为a的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为
如图所示,墙上挂有边长为a的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为| a |
| 2 |
A、
| ||
B、1-
| ||
C、1-
| ||
| D、与a的取值有关 |