题目内容
荆州护城河受污染,其河水的容量为υ立方米,每天流人护城河的水量等于流出护城河的水量,现假设下雨和蒸发平衡,且污染物和湖水均匀混合 用f(t)=p(1-e-
)+f(0)e-
,(p≥0)表示t时刻一立方米河水中所含污染物的克数(我们称其为河水污染的质量分数)f(0)表示河水污染的初始质量分数.当河水污染质量分数为常数时,则其河水污染的初始质量分数为( )
| t |
| v |
| t |
| v |
| A、p | ||
| B、υ | ||
C、e-
| ||
D、e-
|
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:由题意可得f(t)=p(1-e-
)+f(0)e-
为常数,化简得p-(p-f(0))e-
为常数,从而得到p-f(0)=0.
| t |
| v |
| t |
| v |
| t |
| v |
解答:
解:由题意可得,
f(t)=p(1-e-
)+f(0)e-
为常数,
即p-(p-f(0))e-
为常数,
故p-f(0)=0,
解得,f(0)=p,
故选A.
f(t)=p(1-e-
| t |
| v |
| t |
| v |
即p-(p-f(0))e-
| t |
| v |
故p-f(0)=0,
解得,f(0)=p,
故选A.
点评:本题考查了学生将实际问题转化为数学问题的能力,属于中档题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
a,b是两条异面直线,且a⊥平面α,b⊥平面β,则α,β的关系是( )
| A、相交 | B、平行 |
| C、相交或平行 | D、垂直 |
某人5次上班途中所花的时间(单位:分钟)分别为x,8,10,11,9.已知这组数据的平均数为10,则其方差为( )
| A、2 | B、4 | C、10 | D、20 |
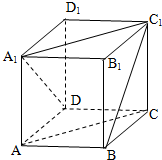 如图,正方体ABCD-A1B1C1D1,异面直线BC1、A1D所成的角的大小为
如图,正方体ABCD-A1B1C1D1,异面直线BC1、A1D所成的角的大小为