题目内容
将抛物线y2=4x按向量
=（1，2）平移后与直线x-2y+m=0相切，则m的值为（ ）
| a |
| A、-1 | B、7 | C、9 | D、1 |
考点：直线与圆锥曲线的关系
专题：圆锥曲线的定义、性质与方程
分析：将抛物线y2=4x按向量
=（1，2）平移后，得（y-2）2=4（x-1），联立
，得y2-12y+4m+8=0，由已知得△=（-12）2-4（4m+8）=0，由此能求出结果．
| a |
|
解答：
解：将抛物线y2=4x按向量
=（1，2）平移后，
得（y-2）2=4（x-1），
即y2-4y-4x+8=0，
联立
，
得y2-12y+4m+8=0，
由已知得△=（-12）2-4（4m+8）=0，
解得m=7．
故选：B．
| a |
得（y-2）2=4（x-1），
即y2-4y-4x+8=0，
联立
|
得y2-12y+4m+8=0，
由已知得△=（-12）2-4（4m+8）=0，
解得m=7．
故选：B．
点评：本题考查满足条件的实数值的求法，是中档题，解题时要认真审题，注意抛物线性质的合理运用．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
在吸烟与患肺病这两个分类变量的计算中，下列说法正确的是（ ）
| A、若K2的观测值为k=6.635，我们有99%的把握认为吸烟与患肺病有关系；那么在100个吸烟的人中必有99人患有肺病 |
| B、从独立性检验可知有99%的把握认为吸烟与患肺病有关系时，我们说某人吸烟，那么他有99%的可能患有肺病 |
| C、若从统计量中求出有95% 的把握认为吸烟与患肺病有关系，是指有5% 的可能性使得推判出现错误 |
| D、以上三种说法都不正确 |
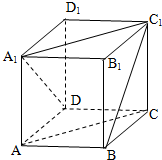如图，正方体ABCD-A1B1C1D1，异面直线BC1、A1D所成的角的大小为