题目内容
sin21999°+cos21999°= ．
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：由同角三角函数基本关系的即可求值．
解答：
解：sin21999°+cos21999°=1．
故答案为：1．
故答案为：1．
点评：本题主要考察了同角三角函数基本关系的运用，属于基本知识的考查．
练习册系列答案
阅读快车系列答案
相关题目
复数（
）6=（ ）
| 1-i |
| 1+i |
| A、-1 | B、1 | C、-i | D、i |
设函数f（x）和g（x）在区间（a，b）内的导函数f′（x）＞g′（x），则在（a，b）内一定有（ ）
| A、f（x）＞g（x） |
| B、f（x）＜g（x） |
| C、f（x）+g（a）＞g（x）+f（a） |
| D、f（x）+g（b）＞g（x）+f（b） |
已知角α终边上一点M的坐标是（-3，4），则sinα+tanα=（ ）
A、-
| ||
B、-
| ||
C、-
| ||
D、
|
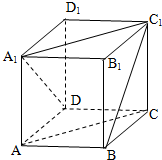如图，正方体ABCD-A1B1C1D1，异面直线BC1、A1D所成的角的大小为